[QQT: PYTHAGORAS, NEWTON, VEDAS]
1/50
Just can’t seem to catch a break, can we? What steaming fresh cow pie is this now?
Okay, let’s do this.
Premise: Stuff originally from Vedic India, falsely attributed to Pythagoras and Newton because world jealous of Indian achievements.
1/50
Just can’t seem to catch a break, can we? What steaming fresh cow pie is this now?
Okay, let’s do this.
Premise: Stuff originally from Vedic India, falsely attributed to Pythagoras and Newton because world jealous of Indian achievements.
![[QQT: PYTHAGORAS, NEWTON, VEDAS]
1/50
Just can’t seem to catch a break, can we? What steaming fresh...](https://pbs.twimg.com/media/FXjPZIxaAAE2HVp.jpg)
2/50
Here, we’ll only talk Pythagoras.
For starters, “Vedic math,” exotic as no doubt it may sound, does not really come from the Vedas. Sure they have some big and small numbers and some very rudimentary geometry, but nothing complex and no algebra.
So what about that theorem?
Here, we’ll only talk Pythagoras.
For starters, “Vedic math,” exotic as no doubt it may sound, does not really come from the Vedas. Sure they have some big and small numbers and some very rudimentary geometry, but nothing complex and no algebra.
So what about that theorem?
3/50
That comes later. The text in question is not a Veda (Samhita), nor even a Brāhmaṇa (Vedic exegesis), but a collection of Śulbasūtras (lit. “codes of the rope”).
Eight treatises by eight different authors, this is the collection where all Vedic math exists.
That comes later. The text in question is not a Veda (Samhita), nor even a Brāhmaṇa (Vedic exegesis), but a collection of Śulbasūtras (lit. “codes of the rope”).
Eight treatises by eight different authors, this is the collection where all Vedic math exists.
4/50
The works deal with mensuration and construction of the various altars or arenas for religious rites. These measurements, back in the day, were done using pieces of strings or śulbas, hence the name.
Do note that all math here was applied geometry.
The works deal with mensuration and construction of the various altars or arenas for religious rites. These measurements, back in the day, were done using pieces of strings or śulbas, hence the name.
Do note that all math here was applied geometry.
5/50
When the Śulbasūtras emerged, we’ll get to in a bit. First, let’s understand what they say about the theorem in question and how.
As I said, there’s eight books.
Among them is one by Baudhāyana—the Baudhāyana Śulba Sūtras, BSS from here on. This is our book of interest.
When the Śulbasūtras emerged, we’ll get to in a bit. First, let’s understand what they say about the theorem in question and how.
As I said, there’s eight books.
Among them is one by Baudhāyana—the Baudhāyana Śulba Sūtras, BSS from here on. This is our book of interest.
6/50
The text devotes itself to the design of what’s called a “mahāvedi,” a kind of sacrificial altar used in Vedic rites.
So one thing is evident: that geometry at this point was fundamental to religion. The design of these vedis and yūpas had zero room for error.
The text devotes itself to the design of what’s called a “mahāvedi,” a kind of sacrificial altar used in Vedic rites.
So one thing is evident: that geometry at this point was fundamental to religion. The design of these vedis and yūpas had zero room for error.
7/50
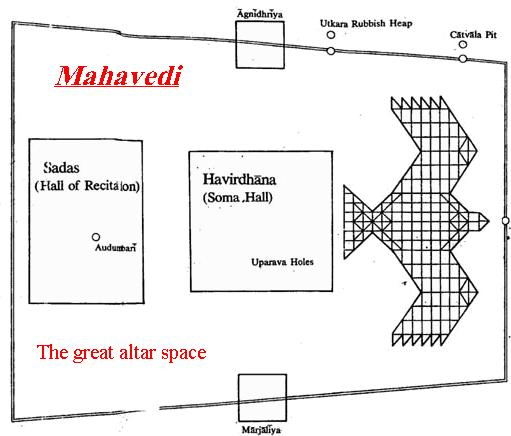
The design and dimensions of the mahāvedi have also been addressed in the Śatapatha Brāhmaṇa, an older Vedic commentary, but it’s only in the Baudhāyana text that the idea has been expounded in detail. The Brāhmaṇa’s geometry is extremely cursory.
The design and dimensions of the mahāvedi have also been addressed in the Śatapatha Brāhmaṇa, an older Vedic commentary, but it’s only in the Baudhāyana text that the idea has been expounded in detail. The Brāhmaṇa’s geometry is extremely cursory.
8/50
So whenever they say Vedic math, they essentially mean geometry and associated algebra as discussed in the BSS corpus, even if unknowingly so.
With that bit out of the way, let’s zoom in to the exact verse.
So whenever they say Vedic math, they essentially mean geometry and associated algebra as discussed in the BSS corpus, even if unknowingly so.
With that bit out of the way, let’s zoom in to the exact verse.
9/50
Do note that Baudhāyana did many kinds of sūtras, including Śulba and Śrauta. Our verse shows up in the former. This distinction is important because the free copies available online are almost always of the Śrauta text and not Śulba.
Now the verse…
Do note that Baudhāyana did many kinds of sūtras, including Śulba and Śrauta. Our verse shows up in the former. This distinction is important because the free copies available online are almost always of the Śrauta text and not Śulba.
Now the verse…
10/50
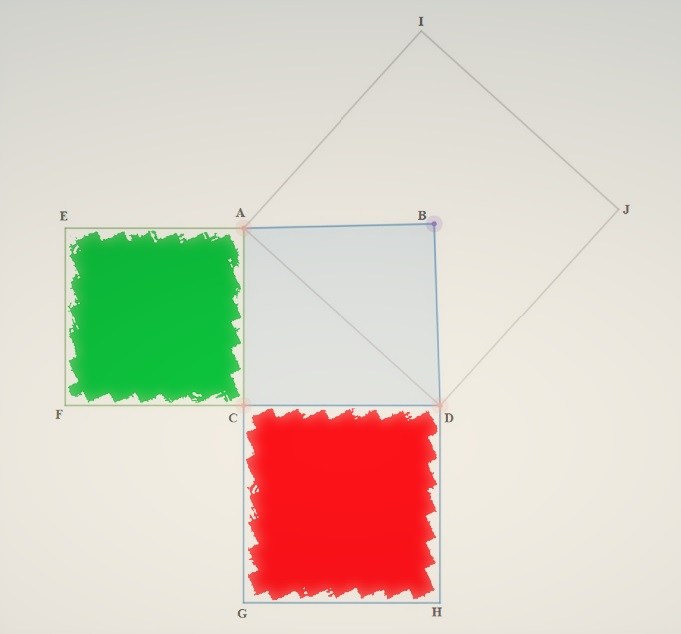
Original (verse 1.12):
दीर्घचतुरश्रस्याक्ष्णया रज्जुः पार्श्वमानी तिर्यग् मानी च यत् पृथग् भूते कुरूतस्तदुभयं करोति॥
Transliteration:
dīrghachatursrasyākṣaṇayā rajjuḥ pārśvamānī, tiryagmānī,
cha yatpṛthagbhūte kurutastadubhayāṅ karoti.
Original (verse 1.12):
दीर्घचतुरश्रस्याक्ष्णया रज्जुः पार्श्वमानी तिर्यग् मानी च यत् पृथग् भूते कुरूतस्तदुभयं करोति॥
Transliteration:
dīrghachatursrasyākṣaṇayā rajjuḥ pārśvamānī, tiryagmānī,
cha yatpṛthagbhūte kurutastadubhayāṅ karoti.
11/50
Translation:
The areas [of the squares] produced separately by the lengths of the breadth of a square together equal the area [of the square] produced by the diagonal.
In other words, using the drawing here,
EAFC + CDGH = ADIJ (areawise)
Translation:
The areas [of the squares] produced separately by the lengths of the breadth of a square together equal the area [of the square] produced by the diagonal.
In other words, using the drawing here,
EAFC + CDGH = ADIJ (areawise)
![11/50
Translation:
The areas [of the squares] produced separately by the lengths of the breadth of a...](https://pbs.twimg.com/media/FXjQQBvaUAEbzsn.png)
![11/50
Translation:
The areas [of the squares] produced separately by the lengths of the breadth of a...](https://pbs.twimg.com/media/FXjQSF6agAI7QCC.png)
![11/50
Translation:
The areas [of the squares] produced separately by the lengths of the breadth of a...](https://pbs.twimg.com/media/FXjQTkbakAAlUwP.png)
12/50
Now, since all quadrilaterals in question are square, the areas can be derived thus:
EAFC = AC²
CDGH = CD²
ADIJ = AD²
Further extrapolating,
AD² = AC² + CD²
i.e.
AD = √(AC² + CD²)
Rings a bell?
Yes, that’s what Pythagoras said.
Now, since all quadrilaterals in question are square, the areas can be derived thus:
EAFC = AC²
CDGH = CD²
ADIJ = AD²
Further extrapolating,
AD² = AC² + CD²
i.e.
AD = √(AC² + CD²)
Rings a bell?
Yes, that’s what Pythagoras said.
13/50
The rule is further illustrated with examples in 1.13 that reads thus:
tāsāṃ trika-catuskayār-dvādaśika-pañcikayāḥ pañca-daśikāṣṭikāyāḥ saptaka-catu-viṃśikayār-dvādaśika-pañcātriṃśikayāḥ pañca-daśikāṣṭi-triśikayārityāsu-upaladhāḥ.
The rule is further illustrated with examples in 1.13 that reads thus:
tāsāṃ trika-catuskayār-dvādaśika-pañcikayāḥ pañca-daśikāṣṭikāyāḥ saptaka-catu-viṃśikayār-dvādaśika-pañcātriṃśikayāḥ pañca-daśikāṣṭi-triśikayārityāsu-upaladhāḥ.
14/50
This verse basically lists out a bunch of values for which the rule had been found to hold. These include 3 and 4; 12 and 5; 15 and 8; 7 and 24; 12 and 35; and 15 and 36.
Evidently, only these values mattered in the relevant context, i.e. altar dimensions.
This verse basically lists out a bunch of values for which the rule had been found to hold. These include 3 and 4; 12 and 5; 15 and 8; 7 and 24; 12 and 35; and 15 and 36.
Evidently, only these values mattered in the relevant context, i.e. altar dimensions.
15/50
Two quick observations here:
1. The theorem is given as a mathematical fiat, a proposition; there’s no proof of derivation.
2. The solutions given are only for very specific numbers listed in the examples.
Two quick observations here:
1. The theorem is given as a mathematical fiat, a proposition; there’s no proof of derivation.
2. The solutions given are only for very specific numbers listed in the examples.
16/50
Naturally, this worked for them. Artisans and priests had no need for other dimensions, so they stuck to the ones given in the sūtra rather than resolving it for other values. In other words, it was all applied geometry with no need for theoretical proofs.
Naturally, this worked for them. Artisans and priests had no need for other dimensions, so they stuck to the ones given in the sūtra rather than resolving it for other values. In other words, it was all applied geometry with no need for theoretical proofs.
17/50
Pythagoras’, on the other hand, was a more comprehensive theorem and covered all pairs. That’s because being theoretical, his theorem also came with detailed step-by-step proof of derivation which could subsequently be resolved for any arbitrary triangle.
Pythagoras’, on the other hand, was a more comprehensive theorem and covered all pairs. That’s because being theoretical, his theorem also came with detailed step-by-step proof of derivation which could subsequently be resolved for any arbitrary triangle.
18/50
And that’s why some may feel it’s only fair that Pythagoras get his name on the equation.
Kind of like the airplane. We know Da Vinci drew the concept centuries before the Wrights, but it’s still the latter that got the credit for showing how it actually works.
And that’s why some may feel it’s only fair that Pythagoras get his name on the equation.
Kind of like the airplane. We know Da Vinci drew the concept centuries before the Wrights, but it’s still the latter that got the credit for showing how it actually works.
19/50
Now chronology-wise, there’s no doubt the BSS beat Pythagoras by centuries. While Pythagoras was born in the 5th century BC, the BSS dates back to at least three centuries earlier.
And that brings us to the age of BSS.
As of now, the consensus stands on 9th century BC.
Now chronology-wise, there’s no doubt the BSS beat Pythagoras by centuries. While Pythagoras was born in the 5th century BC, the BSS dates back to at least three centuries earlier.
And that brings us to the age of BSS.
As of now, the consensus stands on 9th century BC.
20/50
How do we know that?
Well, right off the bat, we know the text was all Sanskrit, albeit an archaic form called Vedic Sanskrit. And the earliest this language has been dated to is around 1800 BC, give or take. So the BSS cannot be older than that.
How do we know that?
Well, right off the bat, we know the text was all Sanskrit, albeit an archaic form called Vedic Sanskrit. And the earliest this language has been dated to is around 1800 BC, give or take. So the BSS cannot be older than that.
21/50
Having established the ceiling, we can further narrow it down based on the dialectical style and grammar employed. I can’t do that, of course, so I defer the call to those who seem to have.
First up is the late David Pingree, a Harvard scholar of Ancient Mathematics.
Having established the ceiling, we can further narrow it down based on the dialectical style and grammar employed. I can’t do that, of course, so I defer the call to those who seem to have.
First up is the late David Pingree, a Harvard scholar of Ancient Mathematics.
22/50
Per Pingree, the work of Baudhāyana predates that of Mānava, another Śulbasūtra author. Extrapolating from that, he places the work to around 500 BC.
This date, however, is contested by many other scholars, Kim Plofker among them.
Per Pingree, the work of Baudhāyana predates that of Mānava, another Śulbasūtra author. Extrapolating from that, he places the work to around 500 BC.
This date, however, is contested by many other scholars, Kim Plofker among them.
23/50
Plofker agrees with the chronology, i.e. Baudhāyana before Mānava, but expands the composition date to a wider range of 800 BC thru 500 BC. His argument is based on the corpus being contemporaneous with Middle Vedic Brāhmaṇas.
Plofker agrees with the chronology, i.e. Baudhāyana before Mānava, but expands the composition date to a wider range of 800 BC thru 500 BC. His argument is based on the corpus being contemporaneous with Middle Vedic Brāhmaṇas.
24/50
Albeit still largely arbitrary, 800 BC seems to enjoy widespread currency amongst scholars both in and outside of India. In the absence of any conclusive evidence to the contrary, I’m sticking to this date for this conversation.
Albeit still largely arbitrary, 800 BC seems to enjoy widespread currency amongst scholars both in and outside of India. In the absence of any conclusive evidence to the contrary, I’m sticking to this date for this conversation.
25/50
So that makes BSS at least 300 years older than Pythagoras. Even if we go by Pingree’s 500 BC, the two only come nearly contemporary at best.
Who gets the credit in that case?
Well, I said “nearly” contemporary because Pythagoras was still 70 years before 500 BC.
So that makes BSS at least 300 years older than Pythagoras. Even if we go by Pingree’s 500 BC, the two only come nearly contemporary at best.
Who gets the credit in that case?
Well, I said “nearly” contemporary because Pythagoras was still 70 years before 500 BC.
26/50
Now, do note that the two cultures hadn’t yet come in contact yet; that wouldn’t happen until around Alexander.
So even if contemporary, there’s no way either would’ve borrowed from the other. This establishes the purely indigenous origins of BSS.
And also Pythagoras.
Now, do note that the two cultures hadn’t yet come in contact yet; that wouldn’t happen until around Alexander.
So even if contemporary, there’s no way either would’ve borrowed from the other. This establishes the purely indigenous origins of BSS.
And also Pythagoras.
27/50
One may debate the assignment of credit in this close call, especially when it’s certain both discoveries were independent of each other, the story isn’t over yet.
But before we get there, let’s introduce the term Pythagorean triplets. This will feature a lot now.
One may debate the assignment of credit in this close call, especially when it’s certain both discoveries were independent of each other, the story isn’t over yet.
But before we get there, let’s introduce the term Pythagorean triplets. This will feature a lot now.
28/50
A Pythagorean triple, or just triple, is any set of three whole numbers that satisfy the theorem a² + b² = c². Here, a, b, and c are, of course, the three sides of a right-angle triangle, c being the hypotenuse.
Take, for instance, the set of 3, 4, and 5:
3² + 4² = 5².
A Pythagorean triple, or just triple, is any set of three whole numbers that satisfy the theorem a² + b² = c². Here, a, b, and c are, of course, the three sides of a right-angle triangle, c being the hypotenuse.
Take, for instance, the set of 3, 4, and 5:
3² + 4² = 5².
29/50
Now we get to the story.
In the early 1920s, a New York publisher named George A. Plimpton bought from an archeology dealer named Edgar J. Banks, a clay tablet excavated from a southern Iraq archeological site of Tell Senkereh.
Now we get to the story.
In the early 1920s, a New York publisher named George A. Plimpton bought from an archeology dealer named Edgar J. Banks, a clay tablet excavated from a southern Iraq archeological site of Tell Senkereh.
30/50
Plimpton subsequently sold it to Columbia University where it still sits to this day. They named the tablet after its seller along with a catalog number—Plimpton 322.
It’s a rather small tablet; less than an inch thick, and could fit in your palm.
Plimpton subsequently sold it to Columbia University where it still sits to this day. They named the tablet after its seller along with a catalog number—Plimpton 322.
It’s a rather small tablet; less than an inch thick, and could fit in your palm.
31/50
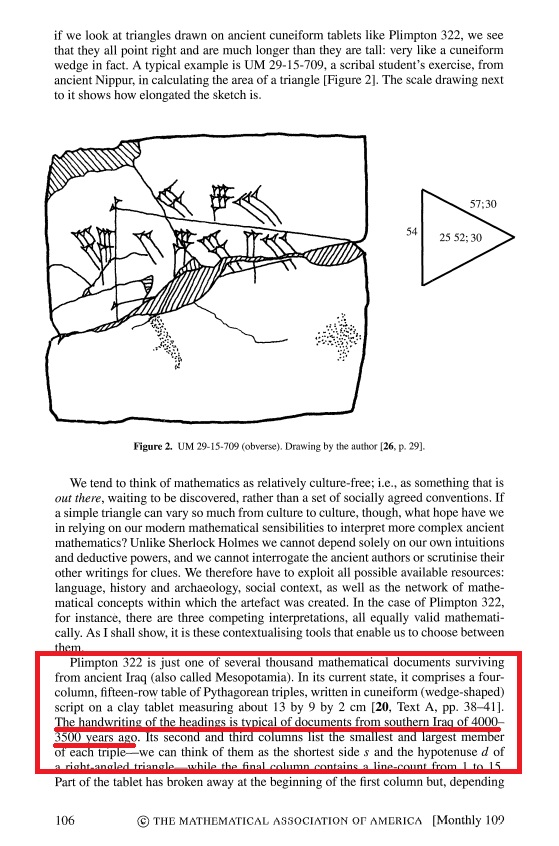
What makes this artifact of interest to this conversation is its contents. Largely intact, save a couple of small chips on the upper left and mid-right, the piece is inscribed with a “spreadsheet” of 16 rows and 4 columns, filled with numerals in Old Babylonian cuneiform.
What makes this artifact of interest to this conversation is its contents. Largely intact, save a couple of small chips on the upper left and mid-right, the piece is inscribed with a “spreadsheet” of 16 rows and 4 columns, filled with numerals in Old Babylonian cuneiform.
32/50
The inscription remained undeciphered until 1945 when the Austrian-American historian and mathematician Otto Neugebauer finally cracked the code and published his findings.
Neugebauer had fled to America in 1939 after openly defying Hitler and inviting persecution.
The inscription remained undeciphered until 1945 when the Austrian-American historian and mathematician Otto Neugebauer finally cracked the code and published his findings.
Neugebauer had fled to America in 1939 after openly defying Hitler and inviting persecution.
33/50
Neugebauer concluded the first row to be a header row and the last column to be a header column with serial numbers, much like a modern Excel sheet done right-to-left (do note that the Mesopotamians wrote right to left).
Neugebauer concluded the first row to be a header row and the last column to be a header column with serial numbers, much like a modern Excel sheet done right-to-left (do note that the Mesopotamians wrote right to left).
34/50
This leaves us with a matrix of 15 rows and 3 columns filled with random positive integers, all in the sexagesimal notation typical of Ancient Mesopotamia.
After closer observation and numerous calculations, Neugebauer also concluded a pattern in this randomness.
This leaves us with a matrix of 15 rows and 3 columns filled with random positive integers, all in the sexagesimal notation typical of Ancient Mesopotamia.
After closer observation and numerous calculations, Neugebauer also concluded a pattern in this randomness.
34/50
To understand his observations, let’s number the columns. Since the writing system is right-to-left, the 4th column is technically the “first.” But since it’s just serial numbers, we’ll ignore it. That leaves us with three columns, first thru third, right to left.
To understand his observations, let’s number the columns. Since the writing system is right-to-left, the 4th column is technically the “first.” But since it’s just serial numbers, we’ll ignore it. That leaves us with three columns, first thru third, right to left.
35/50
Neugebauer noted that, for any given row, if he squared the value in column III (the “first” non-header column) and subtracted from it the square of value in column II, the difference was itself a perfect square.
Sounds like a familiar pattern?
Pythagorean triples!
Neugebauer noted that, for any given row, if he squared the value in column III (the “first” non-header column) and subtracted from it the square of value in column II, the difference was itself a perfect square.
Sounds like a familiar pattern?
Pythagorean triples!
36/50
That leaves us with a total of fifteen triples.
Baudhāyana gave six.
The only semantic difference between Baudhāyana’s examples and the Mesopotamians’ is that in the formula,
d² = s² + l²,
Baudhāyana gives s and l, whereas Plimpton 322 gives d and s.
That leaves us with a total of fifteen triples.
Baudhāyana gave six.
The only semantic difference between Baudhāyana’s examples and the Mesopotamians’ is that in the formula,
d² = s² + l²,
Baudhāyana gives s and l, whereas Plimpton 322 gives d and s.
37/50
Just like Baudhāyana, the Mesopotamians offer no proof of deduction. All they give is a set of arbitrary values that fit the rule, which is understandable given their preoccupation with practical application rather than theoretical inquiry.
Just like Baudhāyana, the Mesopotamians offer no proof of deduction. All they give is a set of arbitrary values that fit the rule, which is understandable given their preoccupation with practical application rather than theoretical inquiry.
38/50
Of course, it’s extremely unlikely that Baudhāyana borrowed knowledge from the Mesopotamians although the exchange between the two civilizations goes back to the IVC times.
But one came before the other. And must one force a credit, it ought to go to that one.
Of course, it’s extremely unlikely that Baudhāyana borrowed knowledge from the Mesopotamians although the exchange between the two civilizations goes back to the IVC times.
But one came before the other. And must one force a credit, it ought to go to that one.
39/50
To recall, Baudhāyana is about 800 BC.
The tablet we just studied, goes back to 1800 BC, give or take. That’s a whopping 1,000 years between the two.
Again, there’s no evidence the Indians learned it from the Babylonians, but if sheer vintage were a yardstick…
To recall, Baudhāyana is about 800 BC.
The tablet we just studied, goes back to 1800 BC, give or take. That’s a whopping 1,000 years between the two.
Again, there’s no evidence the Indians learned it from the Babylonians, but if sheer vintage were a yardstick…
40/50
Things still don’t stop here.
Enter the Berlin Papyrus, more accurately Berlin Papyrus 6619.
Albeit the tablet remains the oldest expression of Pythagoras’ rule, the papyrus, too, beats Baudhāyana by a good half millennium, if not more.
Things still don’t stop here.
Enter the Berlin Papyrus, more accurately Berlin Papyrus 6619.
Albeit the tablet remains the oldest expression of Pythagoras’ rule, the papyrus, too, beats Baudhāyana by a good half millennium, if not more.
41/50
Despite the name, the papyrus comes from Ancient Egypt and has nothing to do with Germany. It’s called Berlin only because that’s its current home.
The fragment is expectedly in Middle-Kingdom hieroglyphics and reads a geometrical problem statement.
Despite the name, the papyrus comes from Ancient Egypt and has nothing to do with Germany. It’s called Berlin only because that’s its current home.
The fragment is expectedly in Middle-Kingdom hieroglyphics and reads a geometrical problem statement.
42/50
The problem roughly translates thus:
“There are two numbers.
One is three-fourths of the other.
The squares of both add up to 100.
What are the numbers?”
In algebraic terms:
b = 3a/4, and
a² + b² = 100
The problem roughly translates thus:
“There are two numbers.
One is three-fourths of the other.
The squares of both add up to 100.
What are the numbers?”
In algebraic terms:
b = 3a/4, and
a² + b² = 100
43/50
Anyone who took math in high school should be able to solve the equations as follows:
a² + (3a/4)² = 100
or, a² + a²(3/4)² = 100
or, a²(1 + 9/16) = 100
or, 25a²/16 = 100
or, (5a/4)² = 10²
or, a = 8
subsequently, b = 6.
Only one problem, the Egyptians didn’t know this.
Anyone who took math in high school should be able to solve the equations as follows:
a² + (3a/4)² = 100
or, a² + a²(3/4)² = 100
or, a²(1 + 9/16) = 100
or, 25a²/16 = 100
or, (5a/4)² = 10²
or, a = 8
subsequently, b = 6.
Only one problem, the Egyptians didn’t know this.
44/50
So how did they solve the problem if not algebraically?
They did it geometrically. The method is called “false proposition.” I will spare you the boring mathematical details but remember, the Egyptians had been doing right-angle triangles since at least 2600 BC.
So how did they solve the problem if not algebraically?
They did it geometrically. The method is called “false proposition.” I will spare you the boring mathematical details but remember, the Egyptians had been doing right-angle triangles since at least 2600 BC.
45/50
But the Egyptian side has only this papyrus fragment to bolster its claim. And the pyramids, of course. The problem discussed above suggests at least one Pythagorean triple, i.e. 6, 8, 10.
But it does.
Again, we don’t know for sure if they borrowed from the Babylonians.
But the Egyptian side has only this papyrus fragment to bolster its claim. And the pyramids, of course. The problem discussed above suggests at least one Pythagorean triple, i.e. 6, 8, 10.
But it does.
Again, we don’t know for sure if they borrowed from the Babylonians.
46/50
But the Babylonians and the Egyptians did make contacts. And so did the Indians and the Babylonians. A transfer of knowledge while not established cannot be completely ruled out.
Setting aside the contentious transfer bit, the Babylonians still predate the Indians.
But the Babylonians and the Egyptians did make contacts. And so did the Indians and the Babylonians. A transfer of knowledge while not established cannot be completely ruled out.
Setting aside the contentious transfer bit, the Babylonians still predate the Indians.
47/50
And so do the Egyptians.
About the latter, while some scholars have placed the fragment in the 13th century BC, there’s also those that push it further back to the 12th dynasty which corresponds to between the 19th and 18th century.
If true, that predates Plimpton 322!
And so do the Egyptians.
About the latter, while some scholars have placed the fragment in the 13th century BC, there’s also those that push it further back to the 12th dynasty which corresponds to between the 19th and 18th century.
If true, that predates Plimpton 322!
48/50
Now the question is, who gets the credit?
And on what qualification?
If it’s vintage, the Egyptians win hands down.
If it’s thoroughness, the Greeks get it.
And that’s assuming everybody came up with the formula independently.
Now the question is, who gets the credit?
And on what qualification?
If it’s vintage, the Egyptians win hands down.
If it’s thoroughness, the Greeks get it.
And that’s assuming everybody came up with the formula independently.
49/50
To be honest, Pythagoras only got his name on the rule because the Romans said so. In fact, the whole idea can be traced back to one man who lived in the first century BC.
Vitruvius.
If the name rings a bell, it’s because you’ve likely seen the “Vitruvius Man.”
To be honest, Pythagoras only got his name on the rule because the Romans said so. In fact, the whole idea can be traced back to one man who lived in the first century BC.
Vitruvius.
If the name rings a bell, it’s because you’ve likely seen the “Vitruvius Man.”
50/50
Be that as it may, the name has now become a matter of convention. You’re free to rename it to Baudhāyana’s theorem or something like that. But do know that neither the Egyptians, nor the Iraqis have any problem calling it Pythagoras’ theorem.
SOURCES: As given in context.
Be that as it may, the name has now become a matter of convention. You’re free to rename it to Baudhāyana’s theorem or something like that. But do know that neither the Egyptians, nor the Iraqis have any problem calling it Pythagoras’ theorem.
SOURCES: As given in context.
Loading suggestions...