Algorithms in Rust:
Here is an implementation of finding the greatest common divisor of n numbers in Rust.
It uses Euclidean division to calculate the GCD of two numbers and recursion to calculate the GCD of n.
No fancy language constructs used, except slices.
Here is an implementation of finding the greatest common divisor of n numbers in Rust.
It uses Euclidean division to calculate the GCD of two numbers and recursion to calculate the GCD of n.
No fancy language constructs used, except slices.
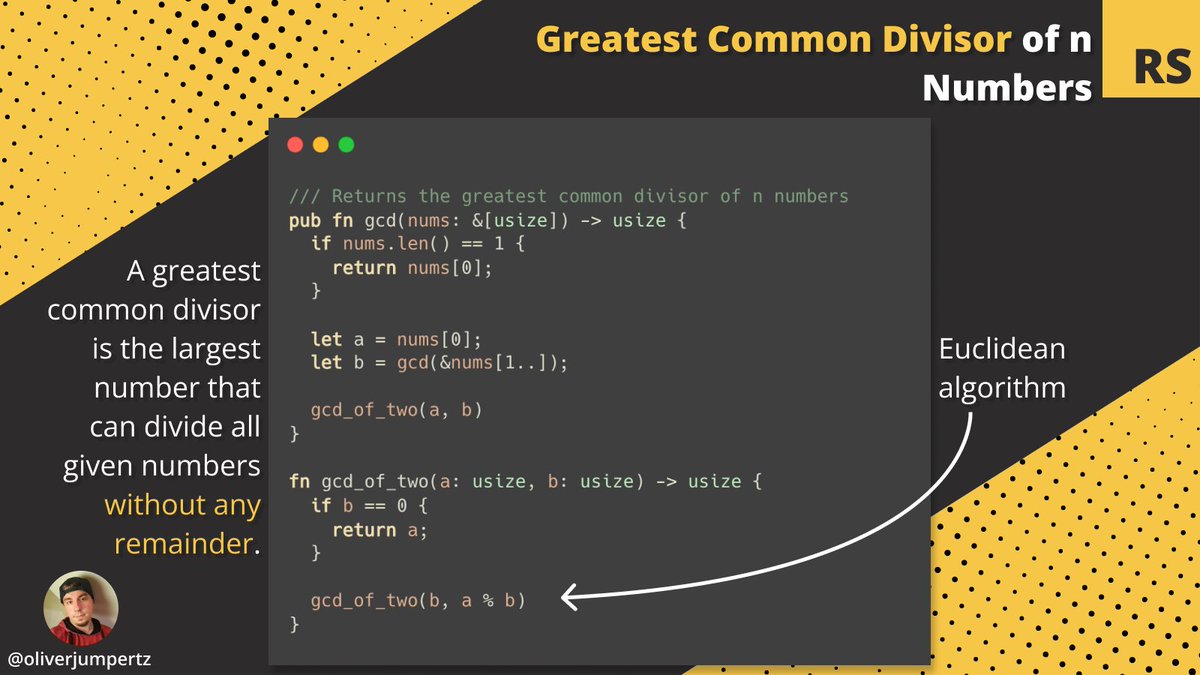
The Euclidean algorithm is based on the principle that the greatest common divisor of two numbers does not change if the larger number is replaced by its difference with the smaller number.
For example, 21 is the GCD of 252 and 105 (as 252 = 21 × 12 and 105 = 21 × 5), and the same number 21 is also the GCD of 105 and 252 − 105 = 147.
Since this replacement reduces the larger of the two numbers, repeating this process gives successively smaller pairs of numbers until the two numbers become equal.
When that occurs, they are the GCD of the original two numbers.
By replacing the repeated subtraction with the modulo operation, you get the exact same outcome while leaving it to your system to efficiently calculate the remainder.
By replacing the repeated subtraction with the modulo operation, you get the exact same outcome while leaving it to your system to efficiently calculate the remainder.
Finding the GCD of n numbers is only this algorithm thought a little further.
If we let n be the number of elements, then the recursion works something like this:
If we let n be the number of elements, then the recursion works something like this:
1. Find the GCD of the elements at n-2 and n-1
2. Use that to find the GCD of the elements at n-3 and the previous GCD
3. Repeat until you reach the very first number
4. Now, you have the GCD in total
2. Use that to find the GCD of the elements at n-3 and the previous GCD
3. Repeat until you reach the very first number
4. Now, you have the GCD in total
Loading suggestions...