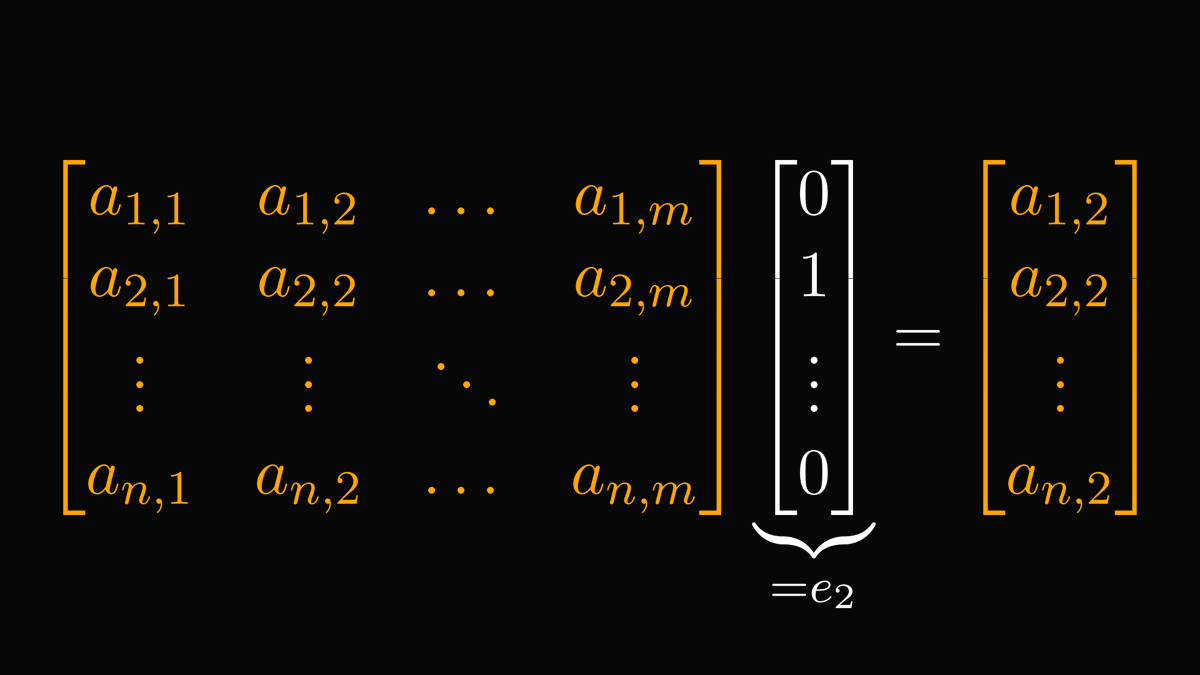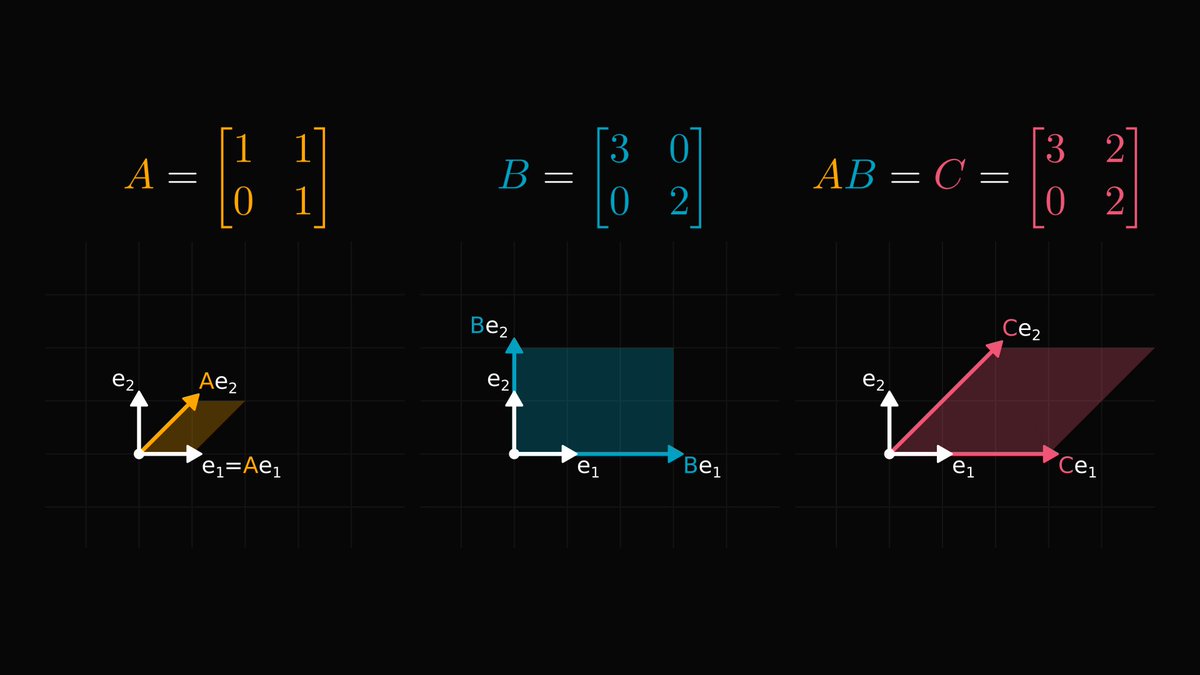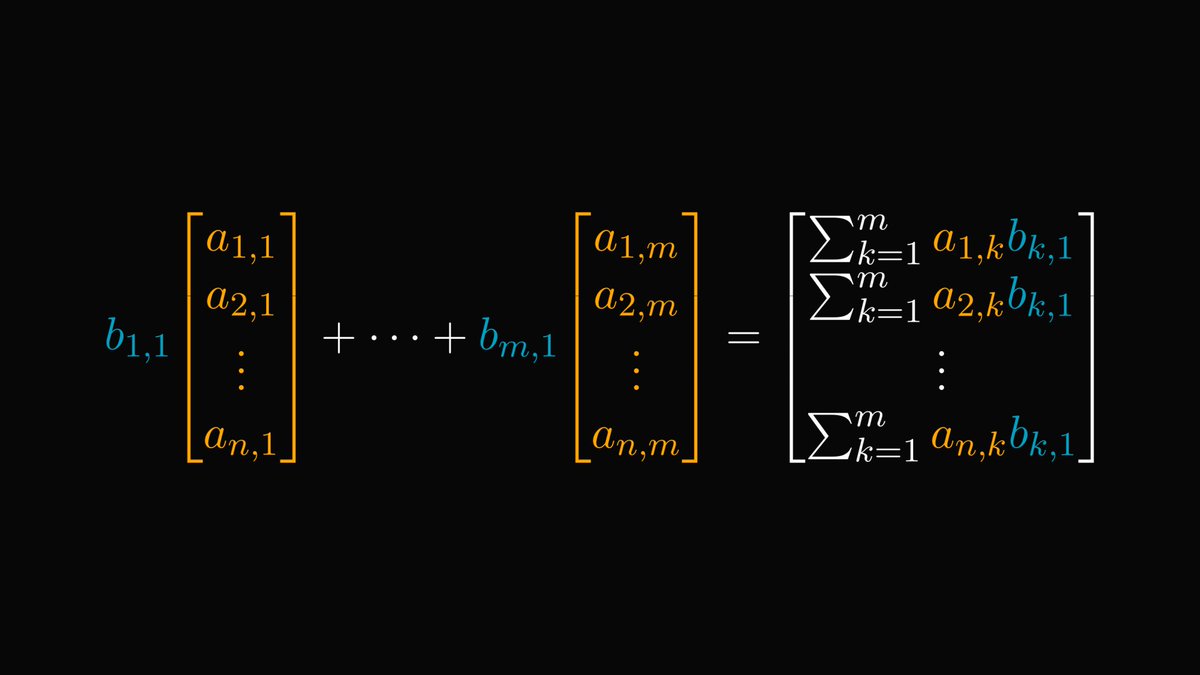There's a stunning, simple explanation behind matrix multiplication.
This is the first time this clicked on my brain, and it will be the best thing you read all week.
Here is a breakdown of the most crucial idea behind modern machine learning:
1/15
This is the first time this clicked on my brain, and it will be the best thing you read all week.
Here is a breakdown of the most crucial idea behind modern machine learning:
1/15
This explanation is courtesy of @TivadarDanka. He allowed me to republish it
3 years ago, he started writing a book about the mathematics of Machine Learning.
It's the best book you'll ever read:
tivadardanka.com
Nobody explains complex ideas like he does.
2/15
3 years ago, he started writing a book about the mathematics of Machine Learning.
It's the best book you'll ever read:
tivadardanka.com
Nobody explains complex ideas like he does.
2/15
Let's start with the raw definition of the product of A and B.
This looks horrible and complicated.
Let's unwrap it step by step.
3/15
This looks horrible and complicated.
Let's unwrap it step by step.
3/15
Here is a quick visualization of multiplying two matrices.
The element in the i-th row and j-th column of AB is the dot product of A's i-th row and B's j-th column.
4/15
The element in the i-th row and j-th column of AB is the dot product of A's i-th row and B's j-th column.
4/15
Now, let's look at a special case:
Multiplying matrix A with a column vector whose first component is 1, and the rest is 0.
Let's name this special vector eβ.
Turns out that the product of A and eβ is the first column of A.
5/15
Multiplying matrix A with a column vector whose first component is 1, and the rest is 0.
Let's name this special vector eβ.
Turns out that the product of A and eβ is the first column of A.
5/15
Similarly, multiplying A with a column vector whose second component is 1 and the rest is 0 yields the second column of A.
That's a pattern!
6/15
That's a pattern!
6/15
By the same logic, we conclude that A times eβ equals the k-th column of A.
7/15
7/15
As every vector is a linear combination of the eβ-s, we can also look at a matrix-vector product as a linear combination of the column vectors.
Make a mental note of this, because it is important.
8/15
Make a mental note of this, because it is important.
8/15
Let's talk in geometric terms.
Matrices are linear transformations: they stretch, skew, rotate, flip, or linearly distort the space.
The images of basis vectors form the columns of the matrix.
We can visualize this in two dimensions:
β’ Aeβ = (-2, 1)
β’ Aeβ = (-1, 2)
9/15
Matrices are linear transformations: they stretch, skew, rotate, flip, or linearly distort the space.
The images of basis vectors form the columns of the matrix.
We can visualize this in two dimensions:
β’ Aeβ = (-2, 1)
β’ Aeβ = (-1, 2)
9/15
From a geometric perspective, the product AB is the same as applying B and then A to our underlying space.
10/15
10/15
Recall that matrix-vector products are linear combinations of column vectors.
With this in mind, we see that the first column of AB is the linear combination of A's columns. (With coefficients from the first column of B.)
11/15
With this in mind, we see that the first column of AB is the linear combination of A's columns. (With coefficients from the first column of B.)
11/15
We can collapse the linear combination into a single vector, resulting in a formula for the first column of AB.
This is straight from the mysterious matrix product formula at the start of this post.
12/15
This is straight from the mysterious matrix product formula at the start of this post.
12/15
We can use the same logic to get an explicit formula to calculate the elements of a matrix product.
13/15
13/15
The power of Linear Algebra is abstracting away the complexity of manipulating data structures like vectors and matrices.
Instead of explicitly dealing with arrays and convoluted sums, we can use simple expressions like AB.
That's a huge deal!
14/15
Instead of explicitly dealing with arrays and convoluted sums, we can use simple expressions like AB.
That's a huge deal!
14/15
The book this came from is crazy good and 100% focused on the math required in machine learning.
You won't find better explanations anywhere else:
tivadardanka.com
Trust me on this one. This is the book you want to read.
15/15
You won't find better explanations anywhere else:
tivadardanka.com
Trust me on this one. This is the book you want to read.
15/15
Loading suggestions...