Indeed, one of the things that new DeFi players fail to grasp is that these protocols that you yield farm on, are not really investments.
The swaps you make are not trades. If an investment is to be understood as one based on fundamental analysis, then the yield farming and the aping that we see, cannot be catagorised as investment, but as speculation, and gambling.
This therefore makes every protocol into a gambling table, where there must always be losers. It is zero sum. Trades are not necessarily zero sum. Investments are not necessarily zero sum. A new protocol popping up is the opening of a new casino. An innovation is a game invented.
You might complain DeFi is not really zero-sum. Yes, in cases where the capital pooled together is sent to yield farm in batches so you save gas, where you LP tgt to earn fees, where you operate as a SPAC, etc.
But honestly, you don't think that or feel that when you ape. You fear being front-run, you fear being dumped on, you care much more about the price than long term vision nonsense. Y'all profit maximalists at heart. Those who aren't are awarded the Crypto Darwin Award.
A fork, is another round of game started. Another game of poker. Another game of chess.
Games can be solved. A solved game is a game whose outcome (win, lose or draw) can be correctly predicted from any position, assuming that both players play perfectly. A game is solved if and only if optimal strategies for any player are all discovered.
Clearly, on a reductive level, solved games are no fun. Tic-tac-toe is a solved game. A game of tic-tac-toe played by two perfectly rational players must result in a draw.
If they were betting money on it, then neither player wins - and in fact the whole endeavour would have in fact cost them time - opportunity cost - so net loss. The rational thing to do when someone offers you play a game of tic-tac-toe is therefore to get lost.
Connect Four is a solved game. And it has been mathematically proven to be first-player-win. If the players were betting on it, then the second player would always lose money. Therefore, if you are offered to play a game of Tic-tac-toe as the second player, you should refuse.
While solved games have a stringent mathematical definition in Game Theory land, we intuitively feel that it is the case, with more plays of the same game, we get increasingly better at a game, and we therefore get closer to the knowledge of optimal strategies.
In simple words, we learn. Evolutionary game theory captures this intuition. Interestingly, the invention and formulation of evolutionary game theory were motivated by the need to explain altruistic behaviours in Darwinian evolution
- that was why @Olympus_ tried to memefy the (3,3) strategy, which is the optimal strategy if all players were rational. Alas, humans are not rational.
gbv.capital
gbv.capital
But given humans are not rational, it would not be exactly accurate to use the mathematical definition of optimal strategies to describe the end state in which players simply stop playing because they know how the gameplay is going to play out.
Olympus forks die not because the game has been solved as players have figured out the strategy optimal according to the mathematical structure of the game, but because players have figured out the strategy optimal according to how players actually play the game.
That’s fine. Let us call a game “resolved” in such a case.
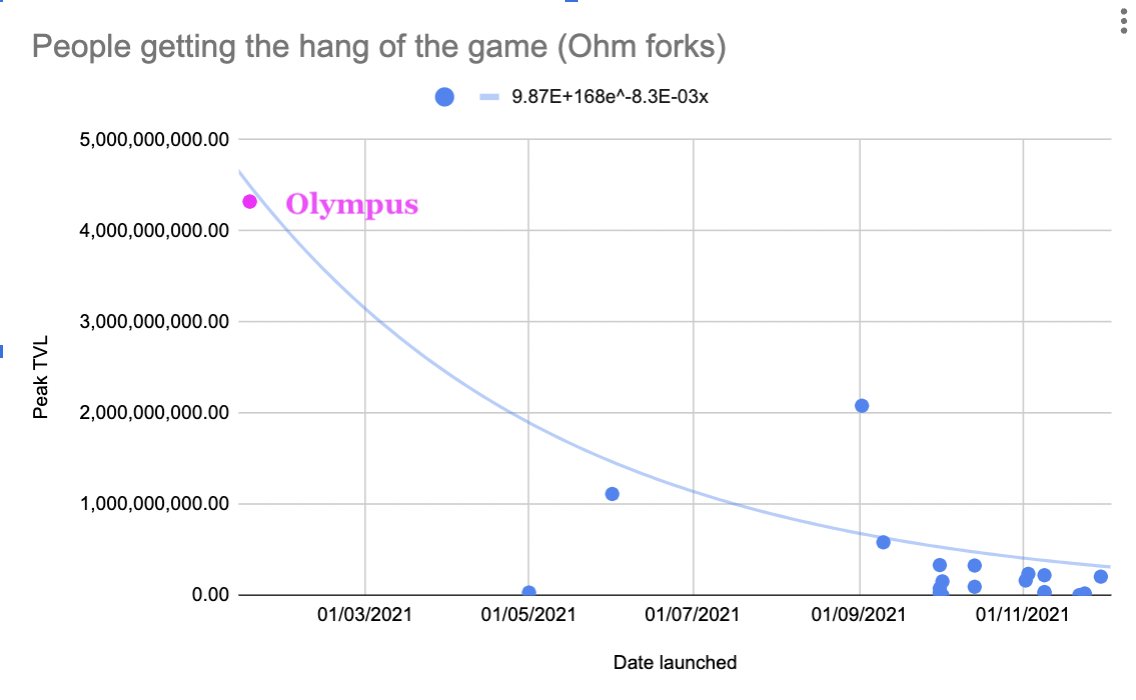
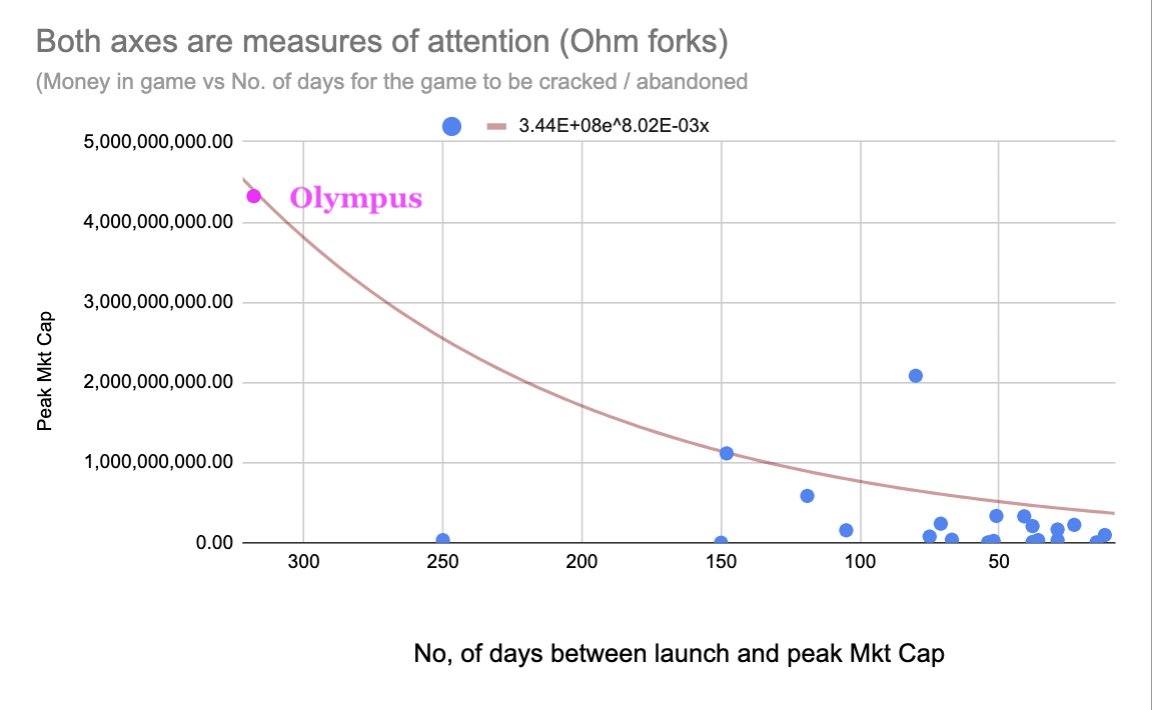
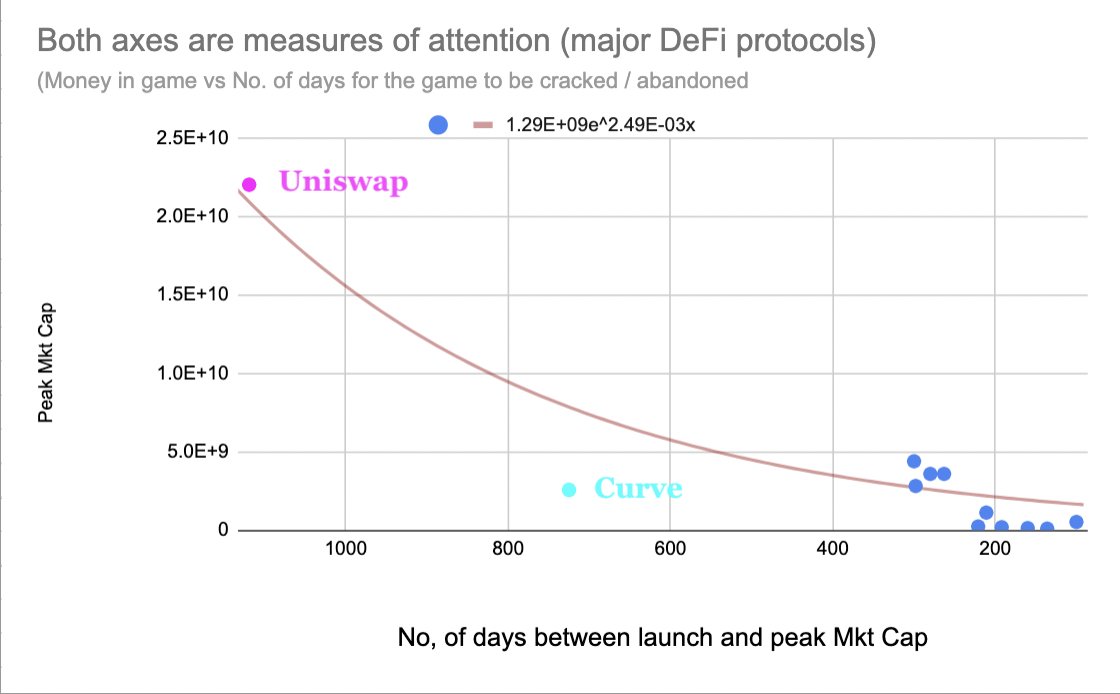
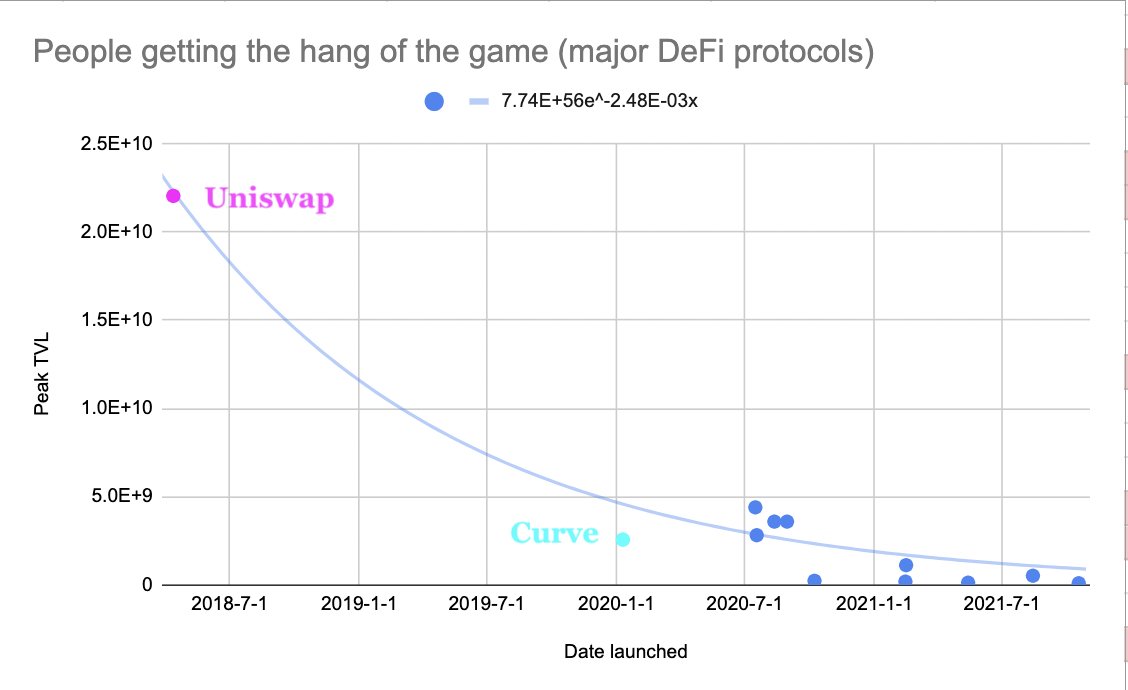
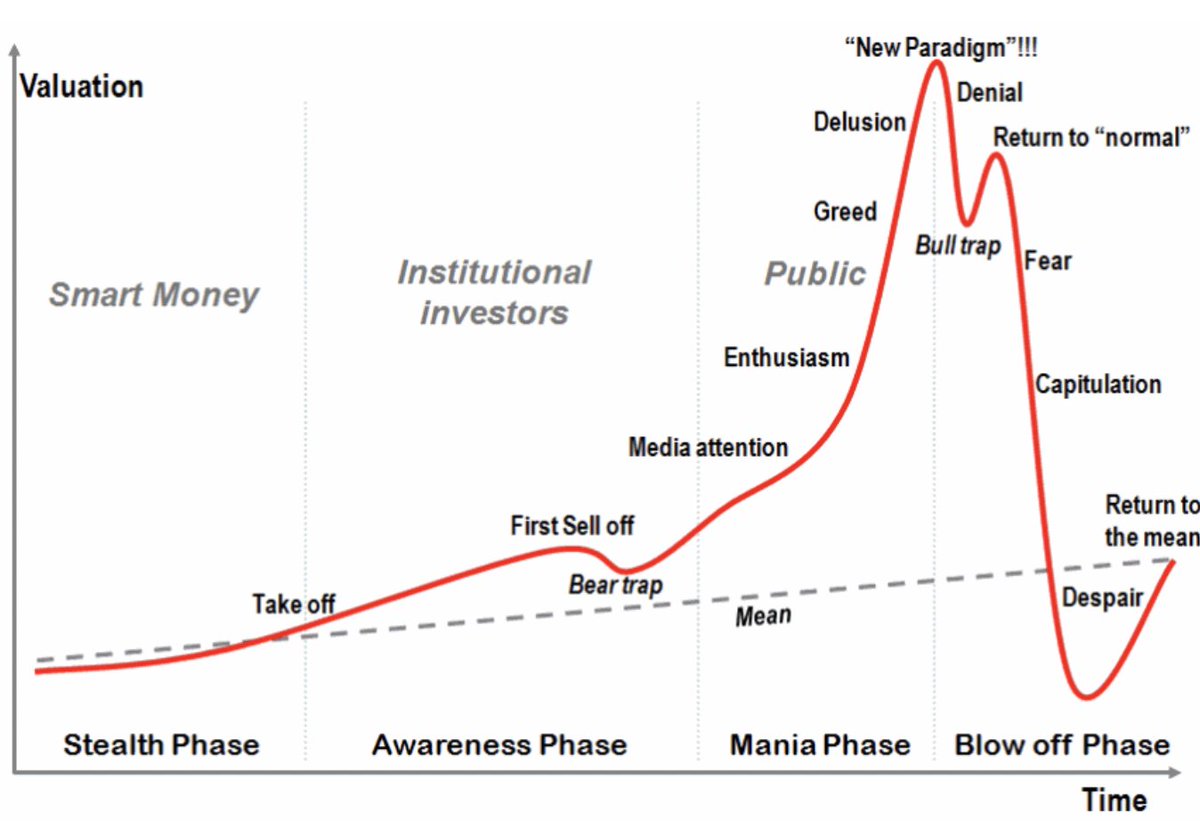
If we view DeFi protocols as games, then it stands to reason that as more forks appear, people play the game better and better, and the speed in which a game is resolved increases. In other words the time in which a game becomes resolved gets shorter and shorter.
We can see this in the graphs below.
We also this kind of decay behaviour when we look at the major primitive DeFi protocols
Whether a game is resolveable should be considered as a different phenomenon to whether a game has exhibited mania. Mania looks like this:
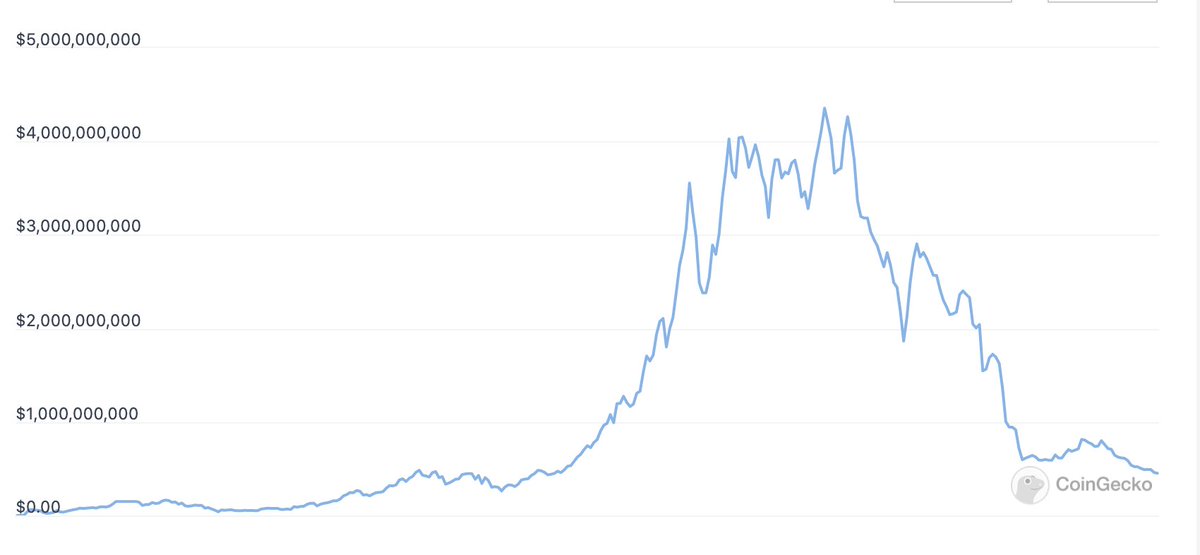
We can probably call Olympus a Resolved Game, and all its instances definitely exhibited mania, but mania is not necessary to a game being resolvable. A game that exhibited mania is not necessarily a resolveable game.
If people just lose interest, and the price crashes, whether the game is resolvable is irrelevant. If I don’t care about the game, I don’t care whether everyone knows how to play and win the game.
However, if a game is resolved, it will definitely exhibit the downward slope of mania.
A game that’s not yet resolved, is likely to exhibit the run-up section of mania - because people don’t know how the game is played and they all feel they might win.
Once the game appears resolved, people will want to get out, either because they figured their strategy has not been the optimal one, or that they are losing already. But if a game is unresolvable, players are more like to stay around, simply because they feel they might win.
Therefore, an unresolvable game is a game in which the fear and capitulation section of the mania curve is extended outwards. An unresolvable game is a game with an infinite half-life.
New iterations of the same unresolvable game can still be launched, in which newer games do not necessarily have jackpots capped by the jackpots of previous iterations.
Projects have an interest in making their projects unresolvable - because if a game is resolved before their tokens unlock, then the fear and capitulation section of the mania curve will have happened before the team tokens unlock.
And given the nature of a resolvable game is that no players will return to the game, what has happened is that the team has built a game with a massive jackpot at one point which they themselves have not enjoyed.
How can a protocol make itself as unresolvable as possible? I can think of three ways to approach it.
(1) Just make it unresolvable: like Chess or Go. This of course assumes unsolvability implies unresolvability. In DeFi protocol design this probably manifests itself as massively increasing the degrees of freedom and the number of possible things you can do with a protocol.
The trouble with this is that it's not clear how you can really do this. What does it look like to replicate the complexity of Chess or Go in a financial vending machine? Is it even possible?
(2) Keep building your protocol and expanding it - V2 bond and inverse bonds in Olympus. The trouble with this is that you have to keep building... building, and building...
(3) Make the Game self-evolving - like how new tokens and projects keep evolving on top of loot, Convex on top of Curve or how you have DeFi protocols built on top of Ethereum, which keeps the Ethereum game running. The great about this is that you are outsourcing your work.
(3) is particularly interesting. I read somewhere before about a "Baselayer Thesis", where successful protocols are necessarily going to be ones where you allow other people to build on top of you.
Also, (3) has a symbiotic relationship with decentralisation it seems. And decentralisation is important for a project because it means you as the founder can leave without rugging.
In practice, one probably needs to do all three, and these tricks to increase unresolvability should be implemented before peak mania, lest you on the dev team become saddled with tokens of a project whose prime has already passed.
While post-top implementation might still introduce new interest, projects of course prefer their market caps to plateau over topping and then go downhill.
One of the interesting developments with @Treasure_DAO is how under the hood, it’s still all DeFi, but it looks and is marketed as a game.
As outlined in its 43 page whitepaper, it has a high number of operations in the protocol with many plausible strategies for players.
(I couldn't find the link to the 43-page whitepaper anymore. All you have are the docs. I suspect the reason why they got rid of it is because they don't want people to break the game too early - they don't want it resolved too early).
docs.treasure.lol
docs.treasure.lol
This seems like a model in which future DeFi protocols might look like. The desire to avoid resolvability, combined with a desire to keep value capture away from TradFi (which also slows down resolvability), it is likely that we will see more protocols like this in the future.
Btw if you want to take a look at the data here it is. It's not super comprehensive but it's good enough to see the relationship. docs.google.com
Full essay here: gbv.capital
Loading suggestions...