1/
Folks, today is July 22'nd. 22/7. Pi Approximation Day.
We all learned in school that 22/7 is a good approximation for pi.
But who came up with it? And how?
It happened ~2300 years ago. In ancient Greece.
Here's the story: ππ
Folks, today is July 22'nd. 22/7. Pi Approximation Day.
We all learned in school that 22/7 is a good approximation for pi.
But who came up with it? And how?
It happened ~2300 years ago. In ancient Greece.
Here's the story: ππ
2/
Before getting to pi, we should first understand the meaning of 2 geometry words: "perimeter" and "area".
Take a piece of paper. Draw any closed shape on it.
The "perimeter" of this shape is the *distance* the tip of your pen traveled as it traced out the shape.
Before getting to pi, we should first understand the meaning of 2 geometry words: "perimeter" and "area".
Take a piece of paper. Draw any closed shape on it.
The "perimeter" of this shape is the *distance* the tip of your pen traveled as it traced out the shape.
3/
By contrast, the "area" of a closed shape is how much *space* the shape takes up on our piece of paper.
In other words, "perimeter" measures a shape's *boundary*. "Area" measures its *interior*.
By contrast, the "area" of a closed shape is how much *space* the shape takes up on our piece of paper.
In other words, "perimeter" measures a shape's *boundary*. "Area" measures its *interior*.
4/
Even centuries ago, "area" and "perimeter" were vital concepts.
For example, if you had a farm and wanted to estimate how much crop it would yield, you'd calculate the farm's *area*.
But if you wanted to build a fence around the farm, you'd calculate its *perimeter*.
Even centuries ago, "area" and "perimeter" were vital concepts.
For example, if you had a farm and wanted to estimate how much crop it would yield, you'd calculate the farm's *area*.
But if you wanted to build a fence around the farm, you'd calculate its *perimeter*.
5/
So, for ages, mathematicians have been trying to devise formulas for the areas and perimeters of various shapes.
They quickly discovered one thing:
If a shape's boundary only has straight LINES, it's EASY to calculate its area and perimeter.
But CURVES are HARD.
So, for ages, mathematicians have been trying to devise formulas for the areas and perimeters of various shapes.
They quickly discovered one thing:
If a shape's boundary only has straight LINES, it's EASY to calculate its area and perimeter.
But CURVES are HARD.
6/
A circle, of course, is one of the most natural and symmetric curved shapes.
So, mathematicians tried for centuries to crack its area and perimeter.
Finally, ~2400 years ago, a Greek mathematician made some headway. His name was Eudoxus.
A circle, of course, is one of the most natural and symmetric curved shapes.
So, mathematicians tried for centuries to crack its area and perimeter.
Finally, ~2400 years ago, a Greek mathematician made some headway. His name was Eudoxus.
7/
Eudoxus discovered that he could cut up a circle into slivers, and then re-arrange these slivers into a "rectangle-like" shape.
This helped Eudoxus derive an equation connecting a circle's area (A), its circumference/perimeter (C), and its radius (r):
A = C * r / 2
Eudoxus discovered that he could cut up a circle into slivers, and then re-arrange these slivers into a "rectangle-like" shape.
This helped Eudoxus derive an equation connecting a circle's area (A), its circumference/perimeter (C), and its radius (r):
A = C * r / 2
8/
In the illustration above, we initially cut up the circle into 12 slivers.
But Eudoxus realized he could go much further.
He could cut up the circle into 24, or 48, or 96, or 1 million slivers!
In the illustration above, we initially cut up the circle into 12 slivers.
But Eudoxus realized he could go much further.
He could cut up the circle into 24, or 48, or 96, or 1 million slivers!
9/
The more slivers Eudoxus used, the "closer" his final shape got to this "mythical" rectangle -- with width C/2 and height r.
But no matter how many slivers, the shape's area always equaled the circle's area A.
After all, the slivers came from cutting up the circle.
The more slivers Eudoxus used, the "closer" his final shape got to this "mythical" rectangle -- with width C/2 and height r.
But no matter how many slivers, the shape's area always equaled the circle's area A.
After all, the slivers came from cutting up the circle.
10/
Eudoxus realized there's only one way to reconcile this:
The circle's area has to be *exactly* (C/2) * r.
Thus, A = (C/2) * r.
This was a landmark moment for math. For the first time, an infinite "cutting up" process was used to reason about a finite thing like a circle.
Eudoxus realized there's only one way to reconcile this:
The circle's area has to be *exactly* (C/2) * r.
Thus, A = (C/2) * r.
This was a landmark moment for math. For the first time, an infinite "cutting up" process was used to reason about a finite thing like a circle.
11/
Notice we've said nothing about pi so far.
All we know so far is: A = (C/2) * r.
We don't yet know that A = pi * (r^2) or that C = 2 * pi * r.
It took another great Greek mathematician -- Euclid -- to piece that together.
Notice we've said nothing about pi so far.
All we know so far is: A = (C/2) * r.
We don't yet know that A = pi * (r^2) or that C = 2 * pi * r.
It took another great Greek mathematician -- Euclid -- to piece that together.
12/
Euclid started with a simple observation.
When we scale a shape by a factor of x, its *area* scales by a factor of "x squared".
For example, doubling the side of a square doesn't just double its area. It quadruples it.
This holds for ALL shapes: triangles, hexagons, etc.
Euclid started with a simple observation.
When we scale a shape by a factor of x, its *area* scales by a factor of "x squared".
For example, doubling the side of a square doesn't just double its area. It quadruples it.
This holds for ALL shapes: triangles, hexagons, etc.
13/
Euclid applied this observation to "regular polygons" inside circles.
To get such "regular polygons":
- We take a circle,
- We put N evenly spaced points on its boundary, and
- We connect the dots.
Like so:
Euclid applied this observation to "regular polygons" inside circles.
To get such "regular polygons":
- We take a circle,
- We put N evenly spaced points on its boundary, and
- We connect the dots.
Like so:
14/
Suppose Euclid had 2 circles -- with radii r1 and r2.
Euclid would then draw 2 regular N-gons: one inside each circle.
Then, by the "scaling of similar shapes" property:
( Area of 1'st N-gon ) / ( Area of 2'nd N-gon )
= ( r1 / r2 ) ^ 2
And this ratio doesn't depend on N.
Suppose Euclid had 2 circles -- with radii r1 and r2.
Euclid would then draw 2 regular N-gons: one inside each circle.
Then, by the "scaling of similar shapes" property:
( Area of 1'st N-gon ) / ( Area of 2'nd N-gon )
= ( r1 / r2 ) ^ 2
And this ratio doesn't depend on N.
15/
Just like Eudoxus, Euclid realized he could take N as high as he liked.
The higher his N, the closer his N-gon areas got to their respective circles' areas.
But the N-gon areas always had the same *ratio*: (r1/r2)^2.
So, the circles' areas HAD to be in that same ratio!
Just like Eudoxus, Euclid realized he could take N as high as he liked.
The higher his N, the closer his N-gon areas got to their respective circles' areas.
But the N-gon areas always had the same *ratio*: (r1/r2)^2.
So, the circles' areas HAD to be in that same ratio!
16/
What this means is:
If we have 2 circles with radii r1 and r2, their areas MUST be in the ratio (r1 / r2) ^ 2.
In other words, the area of a circle is proportional to the *square* of its radius.
And this *proportionality* constant is what we call "pi".
What this means is:
If we have 2 circles with radii r1 and r2, their areas MUST be in the ratio (r1 / r2) ^ 2.
In other words, the area of a circle is proportional to the *square* of its radius.
And this *proportionality* constant is what we call "pi".
17/
So, we have our famous area and circumference (perimeter) formulas that use pi:
A = pi * (r ^ 2) and C = 2 * pi * r.
But so far, we've said nothing about how *big* pi is.
We don't know it's approximately 22/7.
Enter Archimedes -- our third great Greek mathematician.
So, we have our famous area and circumference (perimeter) formulas that use pi:
A = pi * (r ^ 2) and C = 2 * pi * r.
But so far, we've said nothing about how *big* pi is.
We don't know it's approximately 22/7.
Enter Archimedes -- our third great Greek mathematician.
18/
Archimedes got even more mileage out of Euclid's ideas.
His key insight: Sure, we can put a regular N-gon inside our circle. But we can ALSO put the circle itself inside a *second* regular N-gon.
That way, we'll have our circle nicely sandwiched between two N-gons!
Archimedes got even more mileage out of Euclid's ideas.
His key insight: Sure, we can put a regular N-gon inside our circle. But we can ALSO put the circle itself inside a *second* regular N-gon.
That way, we'll have our circle nicely sandwiched between two N-gons!
19/
We can use this "Archimedes sandwich" to approximate pi as closely as we like.
It's how Archimedes got 22/7.
Again, the nub is in increasing our N.
As we take N higher, our outer and inner N-gons come closer -- *always* keeping the circle sandwiched between them.
We can use this "Archimedes sandwich" to approximate pi as closely as we like.
It's how Archimedes got 22/7.
Again, the nub is in increasing our N.
As we take N higher, our outer and inner N-gons come closer -- *always* keeping the circle sandwiched between them.
20/
And as that happens, our N-gon perimeters become better and better approximations to the circle's circumference.
And that can be used to approximate pi more and more closely.
Here's how it works:
And as that happens, our N-gon perimeters become better and better approximations to the circle's circumference.
And that can be used to approximate pi more and more closely.
Here's how it works:
21/
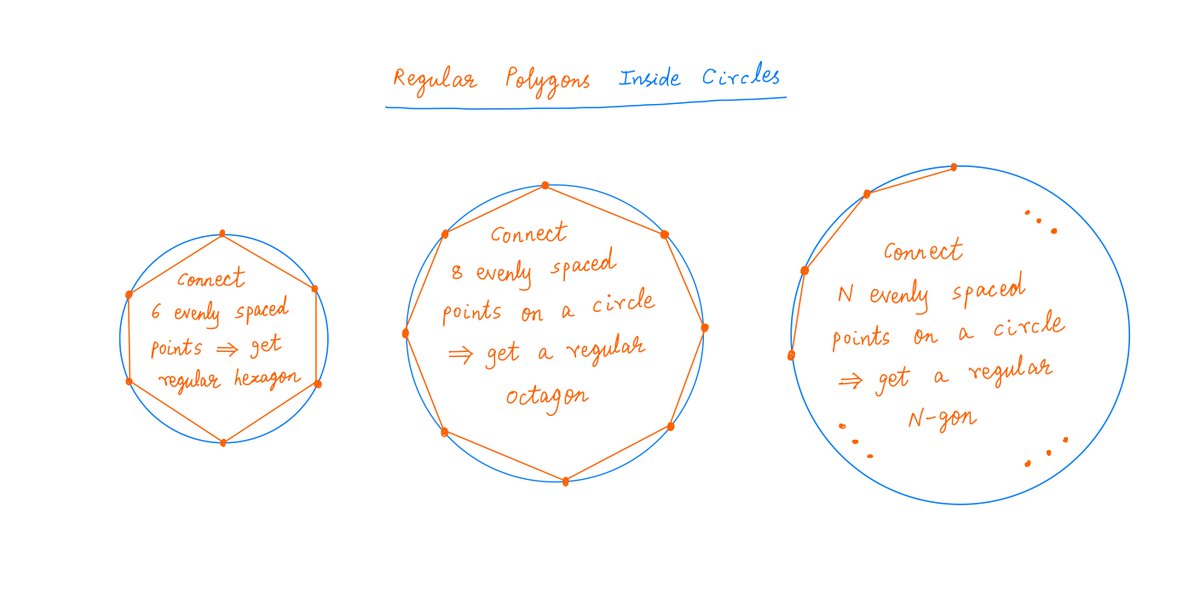
The only part of this approximation scheme we haven't covered is how to calculate a_N and b_N -- the sides of our inner and outer N-gons.
Archimedes solved this brilliantly.
He developed what computer scientists today call an "iterative algorithm" to find a_N and b_N.
The only part of this approximation scheme we haven't covered is how to calculate a_N and b_N -- the sides of our inner and outer N-gons.
Archimedes solved this brilliantly.
He developed what computer scientists today call an "iterative algorithm" to find a_N and b_N.
22/
Here's the idea.
First find a_6. This is easy enough. All it takes is some geometry involving hexagons.
Now, *use* a_6 to *calculate* a_12.
Then, *use* a_12 to *calculate* a_24.
Keep going as long as you like.
And similarly for b_6, b_12, b_24, etc.
Formulas:
Here's the idea.
First find a_6. This is easy enough. All it takes is some geometry involving hexagons.
Now, *use* a_6 to *calculate* a_12.
Then, *use* a_12 to *calculate* a_24.
Keep going as long as you like.
And similarly for b_6, b_12, b_24, etc.
Formulas:
23/
If you're curious how Archimedes got these formulas:
He essentially applied Pythagoras's theorem repeatedly.
Here's the math. But don't worry: you won't need it for the rest of this thread. Feel free to skip it. There will be no quiz. :-)
If you're curious how Archimedes got these formulas:
He essentially applied Pythagoras's theorem repeatedly.
Here's the math. But don't worry: you won't need it for the rest of this thread. Feel free to skip it. There will be no quiz. :-)
24/
~2300 years ago, Archimedes didn't have an easy way to calculate the square roots his formulas demanded.
It took him *months* of tedious calculations to come up with his 22/7 gem.
For that, he had to go to N=96 -- ie, inner and outer polygons containing 96 sides each!
~2300 years ago, Archimedes didn't have an easy way to calculate the square roots his formulas demanded.
It took him *months* of tedious calculations to come up with his 22/7 gem.
For that, he had to go to N=96 -- ie, inner and outer polygons containing 96 sides each!
25/
Today, we can implement Archimedes's logic in like 10 lines of Python.
Archimedes went up to 96-sided polygons. It took him months.
Our Python code goes up to ~100-million sided polygons. In milli-seconds.
How far we've come. And yet, how relevant Archimedes still is!
Today, we can implement Archimedes's logic in like 10 lines of Python.
Archimedes went up to 96-sided polygons. It took him months.
Our Python code goes up to ~100-million sided polygons. In milli-seconds.
How far we've come. And yet, how relevant Archimedes still is!
26/
I'll leave you with a few resources to learn more.
Prof. Steven Strogatz's outstanding book, Infinite Powers, contains some pi history.
It's also a lovely introduction to calculus -- for non-mathematicians.
(h/t @stevenstrogatz)
amazon.com
I'll leave you with a few resources to learn more.
Prof. Steven Strogatz's outstanding book, Infinite Powers, contains some pi history.
It's also a lovely introduction to calculus -- for non-mathematicians.
(h/t @stevenstrogatz)
amazon.com
27/
This ~18 minute video by @veritasium beautifully describes how Isaac Newton discovered a completely new method to calculate pi -- one that's far more powerful than Archimedes's.
youtube.com
This ~18 minute video by @veritasium beautifully describes how Isaac Newton discovered a completely new method to calculate pi -- one that's far more powerful than Archimedes's.
youtube.com
28/
We often see headlines like:
"New research calculates pi to X trillion digits"
If you're curious about the methods these researchers use to find so many digits of pi, read this book: Pi Unleashed.
amazon.com
We often see headlines like:
"New research calculates pi to X trillion digits"
If you're curious about the methods these researchers use to find so many digits of pi, read this book: Pi Unleashed.
amazon.com
29/
Thank you very much for reading all the way to the end.
If you thought this thread was long, you have no idea how long pi goes on for!
/End
Thank you very much for reading all the way to the end.
If you thought this thread was long, you have no idea how long pi goes on for!
/End
Loading suggestions...