[THREAD] Comment atteindre la liberté financière - Le secret des intérêts composés.
![[THREAD] Comment atteindre la liberté financière - Le secret des intérêts composés. https://t.co/ymW...](https://pbs.twimg.com/media/FaiS9AGXkAAf6kM.jpg)
Devenir millionnaire en 20 ans, la recette est simple, du temps et un peu d'argent.
Il suffit de mettre chaque mois un peu d'argent de côté, d'être patient et de répéter l'opération aussi longtemps que possible jusqu'à obtenir le montant souhaité.
Il suffit de mettre chaque mois un peu d'argent de côté, d'être patient et de répéter l'opération aussi longtemps que possible jusqu'à obtenir le montant souhaité.
Pour bien comprendre comment fonctionnent les intérêts composés il faut comprendre d'abord ce qu'est un intérêt, pour calculer ça, rien de plus facile,
il suffit d'appliquer un pourcentage (Exemple: 6%) annoncé sur le capital de départ, et le multiplier par le nombre d'années de placement, sur un an 1000$ à 6 %, nous donne 60$ d'intérêts mais chaque année les 60$ sont retirés du capital de départ.
Et c'est la ou réside le problème des intérêts, le capital de départ ne varie pas, ce qui nous fait 1200$ en + de 1000$ = 2200 en 20 ans, on va pas se mentir c'est nul, même très nul.
Mais imaginez que vous rajoutez chaque mois, les intérêts en plus sur votre d'investissement de 1000$, nous tombons alors dans le monde merveilleux des intérêts composés.
Pour la deuxième année, le pourcentage ne s'applique plus sur 1000$ mais sur 1060$ et ainsi de suite, chaque année le taux d'intérêt va s'appliquer sur un capital gonflé par les intérêts des années précédentes.
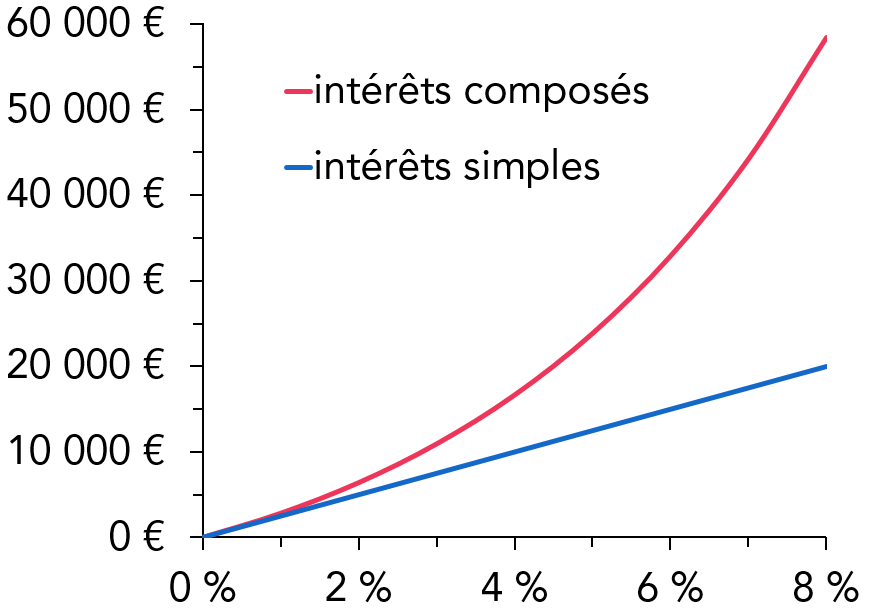
En 20 ans, 1000$ se sera transformé en 3207$, c'est deux, fois, plus qu'avec les intérêts simple qu'on a vu plus haut, mais attendez,
imaginez qu'en plus de ça, au lieu de faire des dépenses inutile que vous regretterez, tel que des cigarettes, des sorties chaque soir, des vêtement trop chère etc..
Vous décidez de rajouter cette argent chaque mois dans votre capital des intérêts composés.
On appel ça l'éducation financièrement.
On appel ça l'éducation financièrement.
Avec un placement de base de 10 000$, en rajoutant 200$ par mois, avec des intérêts de 10% par ans, en 30 ans, vous arrivez à un total de 621 443,41$, en 35 ans, vous êtes millionnaire.
Si vous pouvez vous le permettre, en rajoutant encore plus d'argent chaque mois/année, vous arriverez au million beaucoup plus vite.
Voilà où réside la puissance des intérêts composés qui a même été qualifiée par Albert Einstein que, "les intérêts composés sont la huitième merveille du monde. Celui qui le comprend, s'enrichit, celui qui ne le comprend pas, le paie ».
Une progression exponentielle que rien ne peut arrêter, un placement à intérêts composés avec des taux constants ne peut qu'augmenter indéfiniment avec le temps.
De plus en plus vite c'est ce que l'on appelle l'effet boule de neige.
De plus en plus vite c'est ce que l'on appelle l'effet boule de neige.
Il y'a des sites qui peuvent faire le calcule pour vous, mais voici le calcule à faire: si vous placez 20000$ à 5 % pendant dix ans alors la formule est la suivante:
Cela ne s'arrête jamais le mouvement continue et accélère Einstein a rapidement identifié une particularité dans l'évolution de la courbe et a appelé le phénomène "la règle des 72"
Elle permet de déterminer très rapidement, combien de temps il vous faudra pour doubler un capital de départ, il suffit de diviser le taux par 72 pour obtenir la duré.
Si vous placez 50000$ à 4 %, il vous faudra diviser 72 par 4, soit 18 ans à attendre avant d'obtenir 100 mille dollars.
Le milliardaire américain Warren buffett, lui l'a bien compris et il a su parfaitement s'en servir puisqu'il a déclaré: "ma richesse vient essentiellement de la combinaison de trois choses vivre en amérique la chance et les intérêts composés".
(je n'en ai pas trop parlé dans mon dernier thread sur Warren Buffett car le tweet fessais déjà 60 tweets).
à la fin du thread vous verrez un lien qui calculera tout pour vous, mais dans la vraie vie, il est rare de rencontrer des rendements totalement fixe pendant des décennies, la bourse varie sans arrêt,
néanmoins, ça vous permettra de vous faire une bonne idée de l'effet boule de neige, mais là où les intérêts composés démontre le plus leur efficacité, c'est sur les marchés boursiers.
Mais la bourse, c'est risqué et les coûts varient sans arrêt, à la hausse mais aussi, à la baisse, on peut y perdre tout son investissement à plus ou moins court terme,
C'est pourquoi, une stratégie qui vise à construire un capital, doit, bannir, toute, opération de spéculation, et sur le long terme les meilleurs rendements sont toujours obtenus avec des actions.
Mais il existe une méthode particulièrement efficace pour faire disparaître les problèmes de volatilité tout en décuplant le pouvoir des intérêts composés,
il s'agit du dca, c'est une technique d’investissement qui consiste à investir un montant fixe, à intervalles réguliers, dans un titre financier, quel que soit son cours. En gros, c'est un investissement programmé.
Plutôt que d'investir une somme importante en une fois, vous investissez sans tenir compte du prix du marché, afin de minimiser le risque de mauvais timing et réduire l’impact de la volatilité.
Vous allons donc, par exemple, verser chaque mois 50 ou 100$ sur une action ou une cryptomonnaie, et cela tout les mois sans tenir compte de rien, vous laissez simplement faire le système et les intérêts s'accumulent année après année.
Le DCA a été particulièrement étudiée est démontrée par les mathématiques financières, les statisticiens, les économistes et l'histoire.
Selon. Nick Maggiulli, directeur des opérations chez le gérant de patrimoine américain Ritholtz wealth management et auteur de blog consacré au dca,
cette technique surperforme de 70 % la méthode qui consiste à mettre de l'argent de côté en attendant les périodes de baisse "BUY THE DIP" pour acheter.
Donc si vous avez 100k $ à investir, il est donc préférable d'acheté pour 10 000$ par mois pendant 10 mois sur tous les actifs très volatils tel que: les actions, les crypto monnaie.
Après, rien de mieux que de s'y connaitre et de DCA durant les chutes mais surtout de vendre aussi les tops des marchés, durant les grosses périodes de hausse, on vend, et durant les périodes de baisse, on achète. mais ça c'est un autre sujet.
Il ne faut pas oublier l'essentiel, laisser le temps faire son oeuvre.
"Avec du temps et de la patience, on vient à bout de tout.
En un mot, comment décrieriez-vous les intérêts composés ?
"Avec du temps et de la patience, on vient à bout de tout.
En un mot, comment décrieriez-vous les intérêts composés ?
Voilà pour ce thread, merci d'avoir lu jusqu'ici, si tu souhaites en apprendre plus sur les cryptos, la finance, n'hésite pas à me suivre juste ici ! @0xFaycy
N'oublie pas de soutenir en lâchant ton like et ton retweet sur le premier tweet du thread.
N'oublie pas de soutenir en lâchant ton like et ton retweet sur le premier tweet du thread.
Loading suggestions...