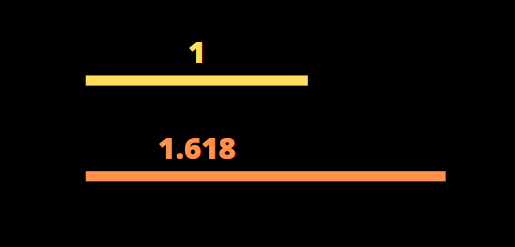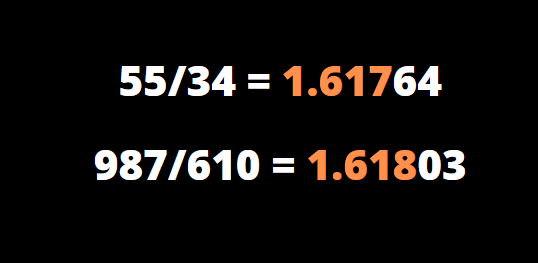[THREAD 🧵] Maths 👨‍💼
La divine proportion : Le NOMBRE D'OR
Tu vas péter ton crâne si tu connais pas 🤯
La divine proportion : Le NOMBRE D'OR
Tu vas péter ton crâne si tu connais pas 🤯
![[THREAD 🧵] Maths 👨‍💼
La divine proportion : Le NOMBRE D'OR
Tu vas péter ton crâne si tu connais pa...](https://pbs.twimg.com/media/FbGgOW8XwAAKvuj.png)
⚠️ DISCLAIMER : Même si les maths te donnent la nausée tu vas tout comprendre t’inquiète pas 🤓
Pense à RT/liker ça fait toujours plaisir 🫶
Allez on y va.
Pense à RT/liker ça fait toujours plaisir 🫶
Allez on y va.
A. Présentation / Origine / Histoire
B. Application
1. Dans l'espace
2. Dans la nourriture
3. Chez les végétaux
4. Chez les animaux
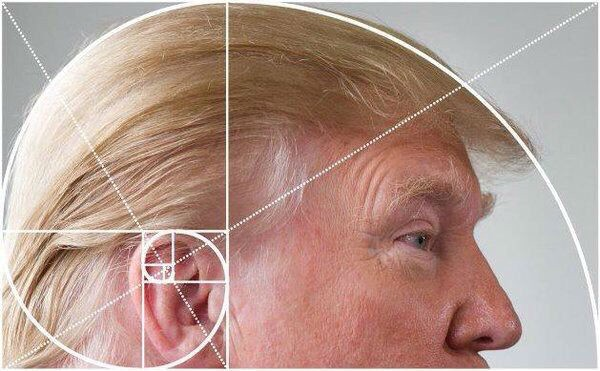
5. Dans le corps humain
6. En architecture
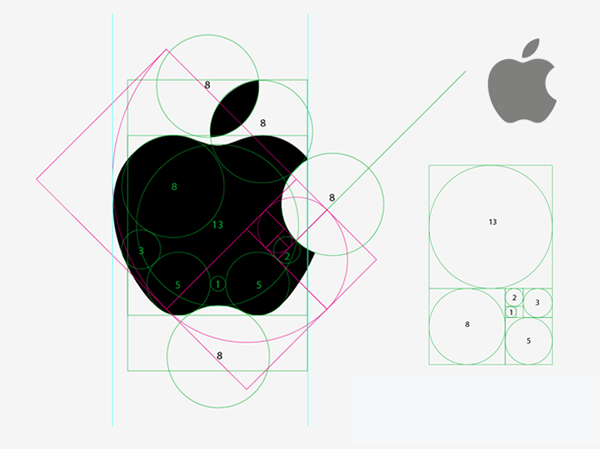
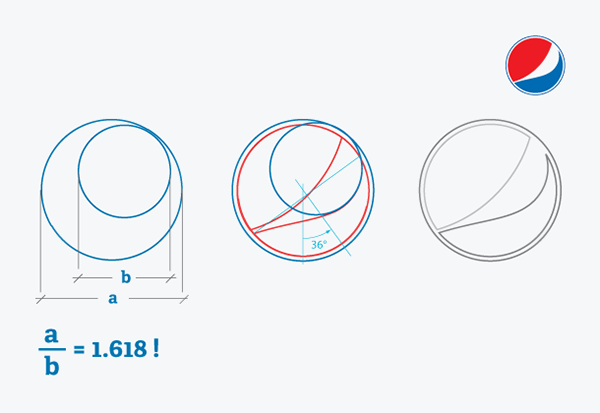
7. Dans le graphisme
8. En finance
C. Conclusion
B. Application
1. Dans l'espace
2. Dans la nourriture
3. Chez les végétaux
4. Chez les animaux
5. Dans le corps humain
6. En architecture
7. Dans le graphisme
8. En finance
C. Conclusion
A. Présentation / Origine / Histoire
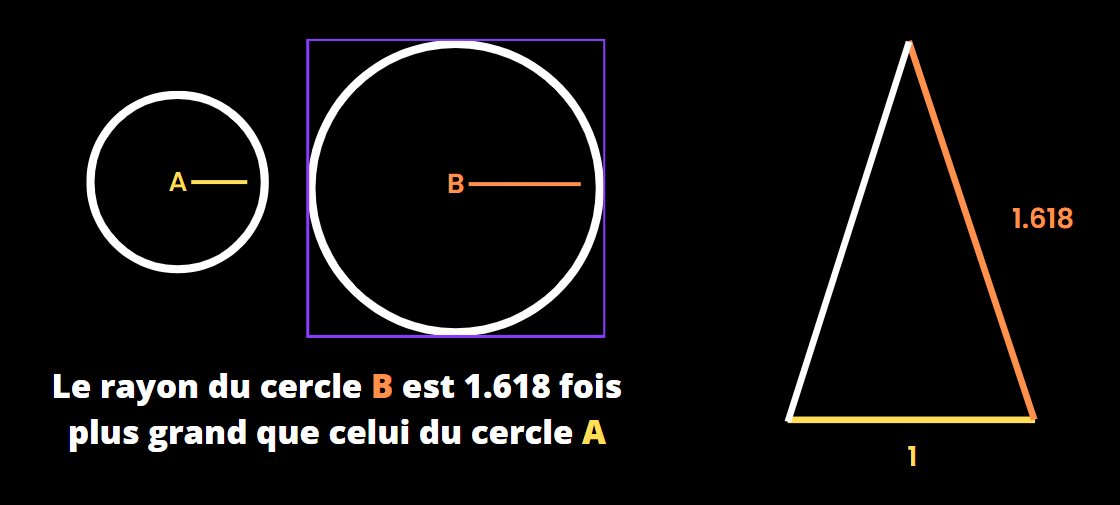
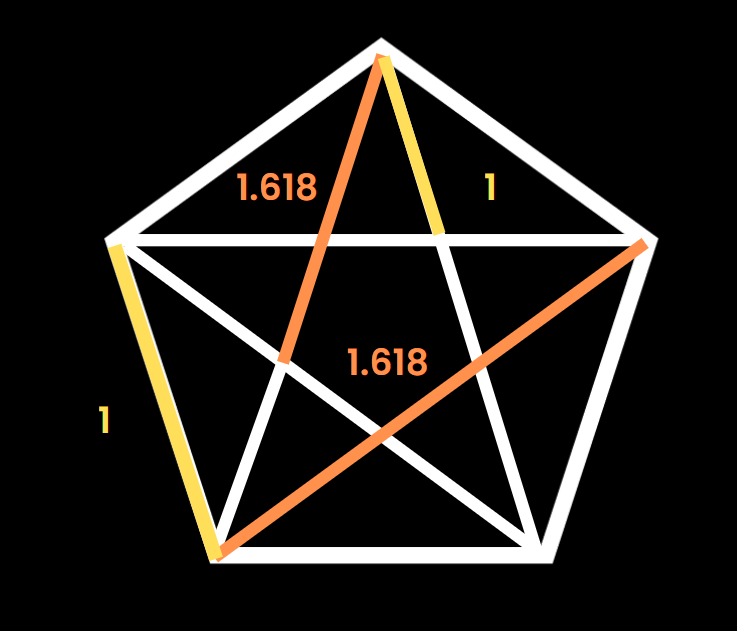
Le nombre d’or ou ratio d’or, est un rapport de proportion qui fascine depuis plusieurs siècles avant J.C. Il donne le nombre irrationnel phi ou Φ, qui équivaut environ à 1,618.
Le nombre d’or ou ratio d’or, est un rapport de proportion qui fascine depuis plusieurs siècles avant J.C. Il donne le nombre irrationnel phi ou Φ, qui équivaut environ à 1,618.
Son nom est dû au sculpteur grec Phidias (430 av. J.C.) qui participa notamment à la décoration du Parthénon sur l’Acropole d’Athènes (on y reviendra plus tard).
Deux segments mesurant respectivement 1 et 1.618 (quelque soit l’unité de mesure) sont donc liés par le nombre d’or.
Première chose assez troublante, le carré du nombre d’or égal à 2.618 soit 1+1.618, les deux termes que nous venons de voir.
Première chose assez troublante, le carré du nombre d’or égal à 2.618 soit 1+1.618, les deux termes que nous venons de voir.
Vous retrouverez ci-dessous ce que l’on appelle un triangle d’or ainsi que deux cercles liés par le nombre d’or.
Le plus incroyable restant tout de mĂŞme le pentagone.
En effet, le nombre d’or est présent naturellement un peu partout dans cette forme géométrique si l’on relie tous les points de cette dernière (vous reconnaitrez ici de nombreux triangles d’or dans cette étoile à 5 branches).
En effet, le nombre d’or est présent naturellement un peu partout dans cette forme géométrique si l’on relie tous les points de cette dernière (vous reconnaitrez ici de nombreux triangles d’or dans cette étoile à 5 branches).
Je pense que vous avez compris le concept donc petit test.
Pour vous, quel est le rectangle le plus “beau” sur l’image ci-dessous ?
Pour vous, quel est le rectangle le plus “beau” sur l’image ci-dessous ?
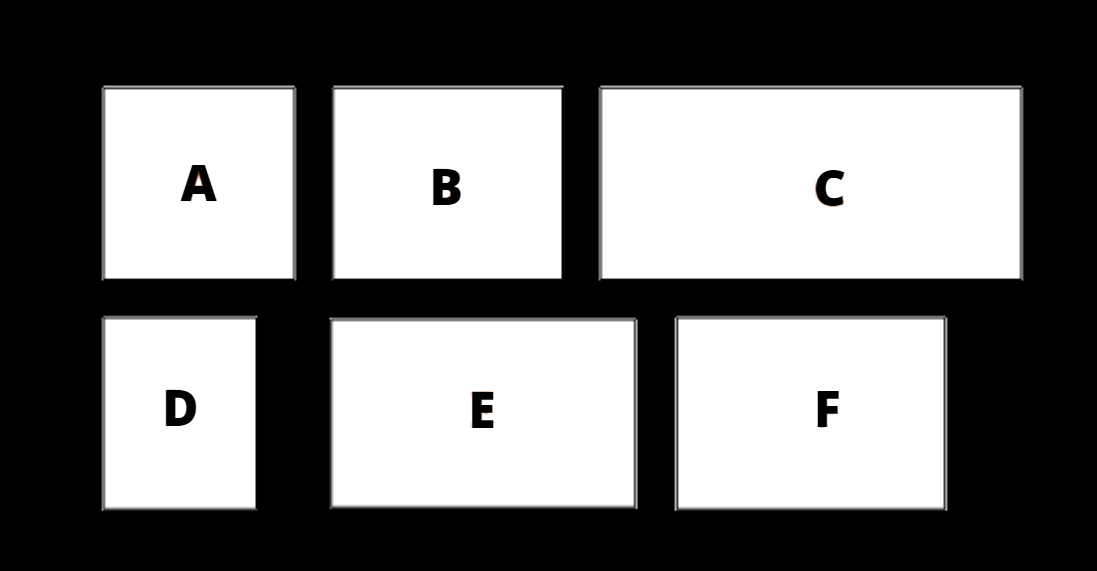
Si vous avez répondu le rectangle “E”, vous êtes tombés sur le rectangle d’or.
C’est celui qui est le plus souvent choisi car ses proportions sont les plus harmonieuses.
C’est celui qui est le plus souvent choisi car ses proportions sont les plus harmonieuses.
Nous allons maintenant aborder la suite de Fibonacci, due au mathématicien italien du XIIIe siècle, Leonardo Pisano, dit Fibonacci.
C’est une série dans laquelle le nombre suivant est la somme des deux précédents.
C’est une série dans laquelle le nombre suivant est la somme des deux précédents.
Très bien, mais le nombre d’or dans tout ça ?
En fait il apparaît si l’on divise un nombre avec celui qui le précède. Plus ils seront élevés, plus le résultat sera précis.
En fait il apparaît si l’on divise un nombre avec celui qui le précède. Plus ils seront élevés, plus le résultat sera précis.
La spirale que vous apercevez ci-dessous et une spirale d’or, une sorte de spirale logarithmique avec un facteur de croissance de 1.618.
Vous voyez d’ailleurs ici que chaque terme appartient à la suite de Fibonacci.
Vous voyez d’ailleurs ici que chaque terme appartient à la suite de Fibonacci.
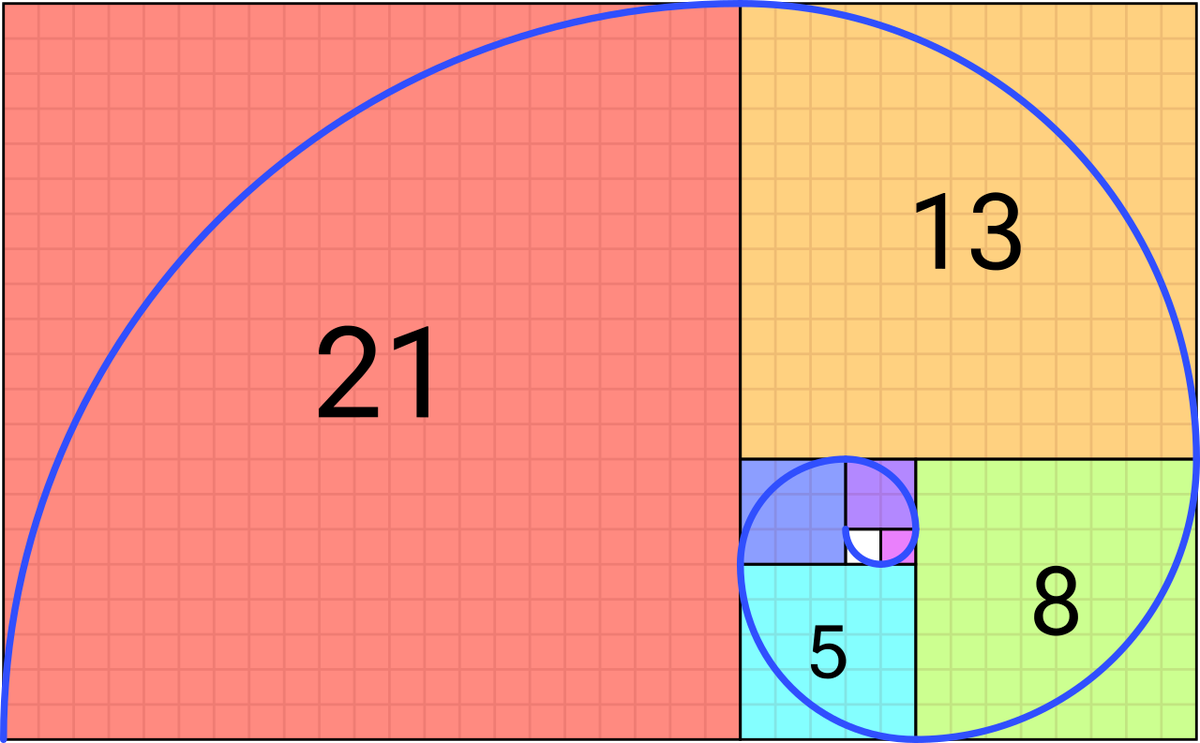
Pour construire cette spirale, on réalise un rectangle d’or dans lequel on trace un grand carré ayant pour côté la largeur du rectangle. On réitère l’action à chaque fois puis, pour finir, on trace ensuite notre spirale en dessinant des quarts de cercle dans chaque carré.
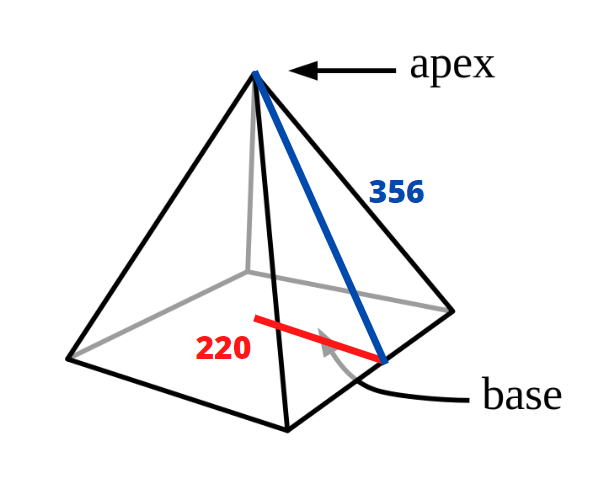
Historiquement, c’est Euclide qui est le premier à écrire sur le sujet, en 300 av. J.C. Mais on retrouve le nombre d’or dans les mesures de la base de la Pyramide de Gizeh en -2560.
Les égyptiens avaient-ils connaissance du nombre d’or à cette époque ou est-ce un simple hasard ?
Les égyptiens avaient-ils connaissance du nombre d’or à cette époque ou est-ce un simple hasard ?
Ok Alex c’est cool mais il sert à quoi ton truc au final ?
Après vous avoir présenté ce qu’est le nombre d’or, nous allons maintenant voir son utilisation concrète.
Après vous avoir présenté ce qu’est le nombre d’or, nous allons maintenant voir son utilisation concrète.
B. Application
1. Dans l'espace
La spirale que je vous ai présenté précédemment vous a sûrement rappelé les différentes galaxies que nous connaissons ou bien encore les tempêtes vues du ciel.
1. Dans l'espace
La spirale que je vous ai présenté précédemment vous a sûrement rappelé les différentes galaxies que nous connaissons ou bien encore les tempêtes vues du ciel.
2. Dans la nourriture
Certains aliments se rapportent également de plus ou moins loin au nombre d’or.
La forme d’un simple œuf se rapporte aussi à la spirale que nous venons d’évoquer.
La peau de l’ananas comprend, elle, trois termes consécutifs de la suite de Fibonacci 👀
Certains aliments se rapportent également de plus ou moins loin au nombre d’or.
La forme d’un simple œuf se rapporte aussi à la spirale que nous venons d’évoquer.
La peau de l’ananas comprend, elle, trois termes consécutifs de la suite de Fibonacci 👀
3. Chez les végétaux
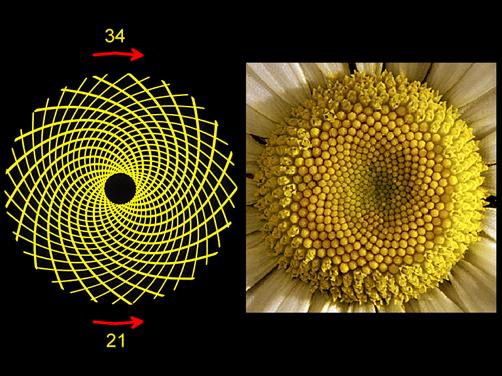
La phyllotaxie, vous connaissez ? C’est une branche de la botanique qui étudie l’ordre dans lequel les feuilles sont implantées sur les branches, tiges de plantes,…
Et justement, si l’ont étudie certains végétaux, on arrive rapidement au nombre d’or.
La phyllotaxie, vous connaissez ? C’est une branche de la botanique qui étudie l’ordre dans lequel les feuilles sont implantées sur les branches, tiges de plantes,…
Et justement, si l’ont étudie certains végétaux, on arrive rapidement au nombre d’or.
Pour la pomme de pin, nous trouvons 8 spirales dans un sens et 13 dans l’autre. Ces deux termes font partie de la suite de Fibonacci.
Même constat pour les pâquerettes, 34 spirales dans un sens et 21 dans l’autre. Et 34/21 = 1.619 soit une précision à quasiment trois décimales.
Même constat pour les pâquerettes, 34 spirales dans un sens et 21 dans l’autre. Et 34/21 = 1.619 soit une précision à quasiment trois décimales.
4. Chez les animaux
Le nautile est sûrement le mollusque le mieux placé sur le sujet : regardez la beauté et la forme de sa coquille !
Les cornes de certains animaux, la queue d’un scorpion ou bien même les tentacules d’une pieuvre se rapportent elles aussi au nombre d’or !
Le nautile est sûrement le mollusque le mieux placé sur le sujet : regardez la beauté et la forme de sa coquille !
Les cornes de certains animaux, la queue d’un scorpion ou bien même les tentacules d’une pieuvre se rapportent elles aussi au nombre d’or !
5. Dans le corps humain
On va commencer par un grand classique : l’Homme de Vitruve de Léonard de Vinci. Le centre de l’œuvre étant le nombril de l’homme, nous pouvons voir que la distance entre le haut de la tête et le nombril est égale à 1 et le reste du corps à 1.618 !
On va commencer par un grand classique : l’Homme de Vitruve de Léonard de Vinci. Le centre de l’œuvre étant le nombril de l’homme, nous pouvons voir que la distance entre le haut de la tête et le nombril est égale à 1 et le reste du corps à 1.618 !
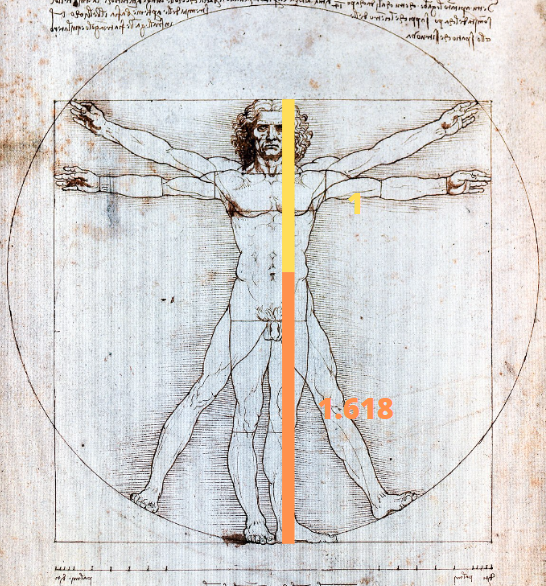
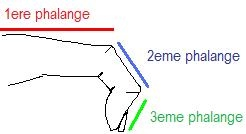
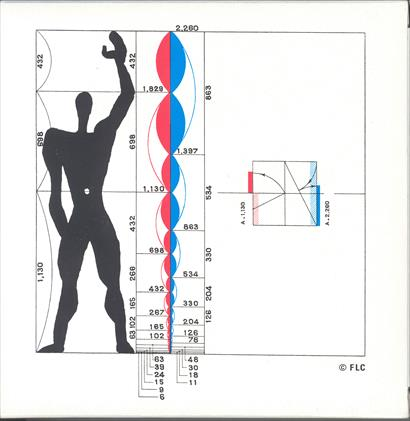
À l’échelle réelle, il est possible de trouver un résultat semblable mais un échantillon constitué d’un grand nombre de personnes serait nécessaire car on ne retrouve pas le nombre d’or en chacun de nous.
Maintenant Ă votre tour.
Maintenant Ă votre tour.
Vous vous regardez tous les jours dans le miroir n’est-ce pas ? Mais avez-vous déjà remarqué cela ?
Regardez votre main…
5 doigts, avec 3 phalanges, reliées par 2 articulations sur 1 main. 1,2,3,5… Vous avez compris je vais pas vous faire un dessin.
Regardez votre main…
5 doigts, avec 3 phalanges, reliées par 2 articulations sur 1 main. 1,2,3,5… Vous avez compris je vais pas vous faire un dessin.
Si vous mesuriez chaque phalange vous tomberiez plus ou moins sur un multiplicateur de 1.618 de l’une à l’autre.
Une autre petite photo sympa aussi 🤪
Une autre petite photo sympa aussi 🤪
6. En architecture
Comme évoqué au début, Phidias (430 av. J.C.) qui participa notamment à la décoration du Parthénon sur l’Acropole d’Athènes.
On le retrouve des rectangles d’or partout sur ce monument car il était à l’époque considéré comme un critère de beauté.
Comme évoqué au début, Phidias (430 av. J.C.) qui participa notamment à la décoration du Parthénon sur l’Acropole d’Athènes.
On le retrouve des rectangles d’or partout sur ce monument car il était à l’époque considéré comme un critère de beauté.
Pour la Pyramide de Gizeh ci-dessous, si l’on divise l’apothème (en bleu) par la demi-base (en rouge), nous avons le calcul suivant en coudées royale (unité de mesure valant environ 52cm) : 356/220 = 1.618
Encore une simple coïncidence ou volonté des Egyptiens ? À vous de voir.
Encore une simple coïncidence ou volonté des Egyptiens ? À vous de voir.
Nous pouvons aussi citer Le Corbusier, un célèbre architecte comme un grand adepte du nombre d’or.
Il a notamment élaboré l’architecture du “United Nations building” de New York qui, comme nous pouvons assez facilement le remarquer, se compose de trois rectangles d’or.
Il a notamment élaboré l’architecture du “United Nations building” de New York qui, comme nous pouvons assez facilement le remarquer, se compose de trois rectangles d’or.
Il est aussi connu pour son “Modulor” (contraction de module et nombre d’or) car toutes les proportions de l’oeuvre sont directement liées au nombre d’or.
7. Dans le graphisme
De grandes entreprises que vous connaissez tous ont aussi leur logo inspiré en toute ou partie par le nombre d’or.
La plus simple à remarquer est National Geographic. La chaîne a tout simplement choisi un rectangle d’or comme logo.
De grandes entreprises que vous connaissez tous ont aussi leur logo inspiré en toute ou partie par le nombre d’or.
La plus simple à remarquer est National Geographic. La chaîne a tout simplement choisi un rectangle d’or comme logo.
Je vous rajoute ci-dessous d’autre images illustrant mes propos.
Certains photographes utilisent aussi le nombre d’or pour placer l’élément principal à un endroit stratégique sur une photo.
Certains photographes utilisent aussi le nombre d’or pour placer l’élément principal à un endroit stratégique sur une photo.
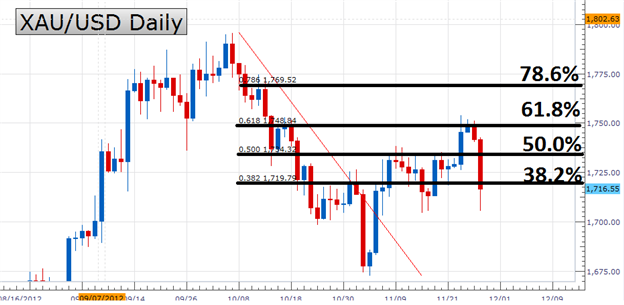
8. En finance
Je ne pouvais pas terminer ce thread sans parler de ma ligne directrice : la finance.
Pour ceux qui l’ignorent, il est possible d’utiliser le nombre d’or et plus précisément la suite de Fibonacci sur les marchés financiers, et cela porte souvent ses fruits.
Je ne pouvais pas terminer ce thread sans parler de ma ligne directrice : la finance.
Pour ceux qui l’ignorent, il est possible d’utiliser le nombre d’or et plus précisément la suite de Fibonacci sur les marchés financiers, et cela porte souvent ses fruits.
On le superpose sur une extension de prix (comme ci-dessous) et différents pourcentages vont se mettre en place.
Certains l’utilisent pour repérer certains cycles, d’autres s’en servent par exemple pour fixer des objectifs et prendre des profits car il s’agit de niveaux où le prix réagit souvent impulsivement.
C. Conclusion
En étant passé par des noms comme “le nombre scandaleux” pour Euclide, “la divine proportion” pour Lucas Pacioli (moine professeur de mathématiques du XVe siècle) et maintenant “le nombre d’or” depuis 1931, ce nombre irrationnel n’a pas fini de faire parler de lui
En étant passé par des noms comme “le nombre scandaleux” pour Euclide, “la divine proportion” pour Lucas Pacioli (moine professeur de mathématiques du XVe siècle) et maintenant “le nombre d’or” depuis 1931, ce nombre irrationnel n’a pas fini de faire parler de lui
de par son côté mystique et ses propriétés fascinantes qui font que l'on peut le retrouver un peu partout dans le très grand (galaxies) et dans le très petit (fleurs,...).
J'aurais Ă©galement pu citer le nombre d'or dans la musique par exemple, mais le fait de le voir partout ne serait-ce pas le voir nulle part ?
Notre imagination peut facilement interpréter les choses et voir le nombre d'or où elle le souhaite.
Notre imagination peut facilement interpréter les choses et voir le nombre d'or où elle le souhaite.
J'ai essayé de faire un thread complet et de qualité tout en restant succinct. J'espère que cela vous aura plu !
On se dit à bientôt pour un prochain thread 🫡
On se dit à bientôt pour un prochain thread 🫡
Loading suggestions...