Professional options traders hedge with delta.
You don't need a PhD to do it.
Or fancy mathematics.
But you do need to know the fundamentals of delta.
Here's what you need to get started:
You don't need a PhD to do it.
Or fancy mathematics.
But you do need to know the fundamentals of delta.
Here's what you need to get started:
A quick primer in case youโre not familiar with delta:
โข Measures the change in the option value for a $1 change in the stock
โข Considered the probability an option will expire in-the-money
โข Ranges from 0 - 1.0 for calls and -1.0 - 0 for puts
So how do traders use delta?
โข Measures the change in the option value for a $1 change in the stock
โข Considered the probability an option will expire in-the-money
โข Ranges from 0 - 1.0 for calls and -1.0 - 0 for puts
So how do traders use delta?
To hedge.
They want exposure to options, not the stock.
So they buy and sell shares to stay neutral - delta tells them how many.
If you buy 1 call option with 0.2 delta, sell 20 shares to delta hedge.
But before you can hedge with delta, you need to know the fundamentals.
They want exposure to options, not the stock.
So they buy and sell shares to stay neutral - delta tells them how many.
If you buy 1 call option with 0.2 delta, sell 20 shares to delta hedge.
But before you can hedge with delta, you need to know the fundamentals.
One last thing:
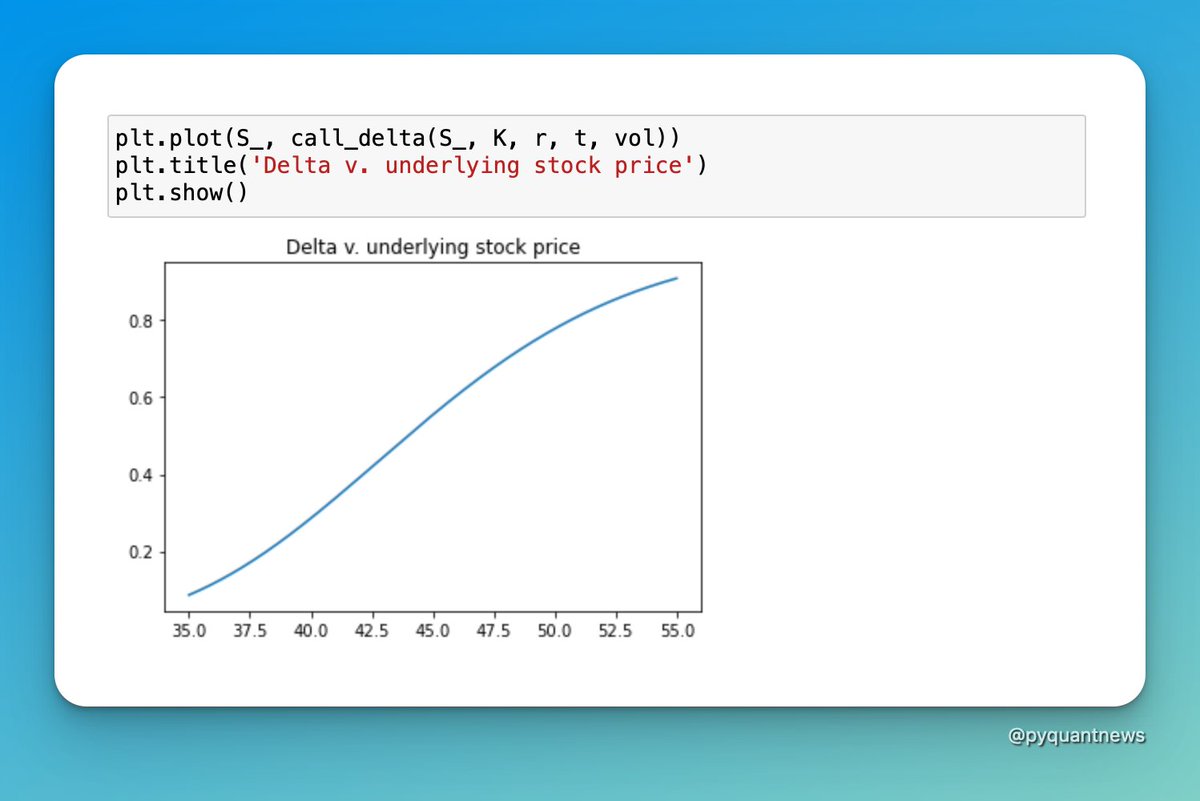
The closer delta is to 1.0 (for calls) or -1.0 (for puts) the more the price of the option moves in tandem with the stock price.
For example:
The value of a call option with a delta of 1.0 will go up $1 for every $1 the stock price goes up.
Ok, let's go!
The closer delta is to 1.0 (for calls) or -1.0 (for puts) the more the price of the option moves in tandem with the stock price.
For example:
The value of a call option with a delta of 1.0 will go up $1 for every $1 the stock price goes up.
Ok, let's go!
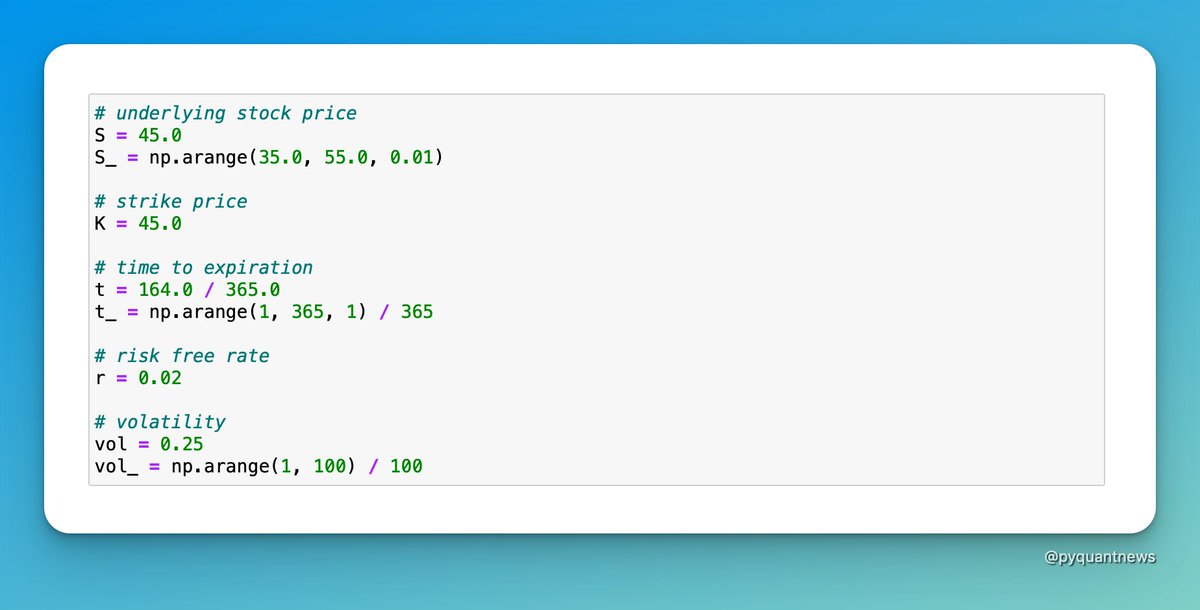
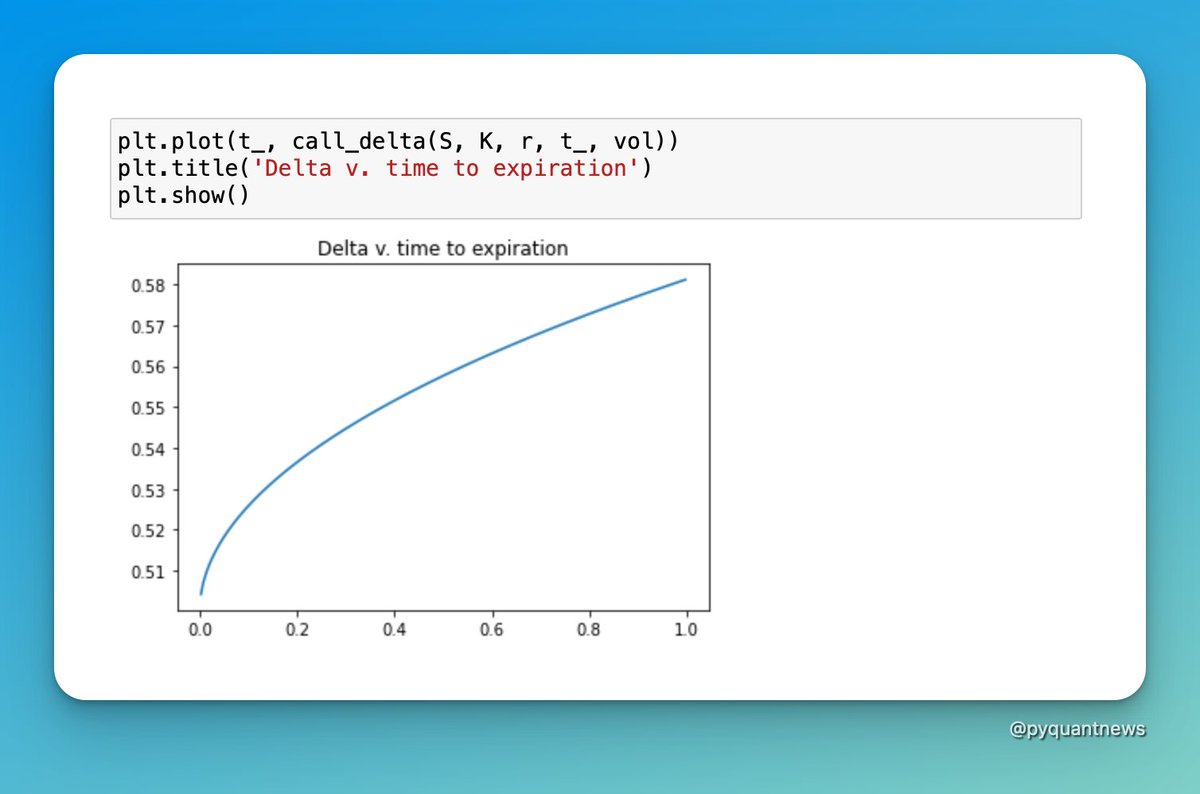
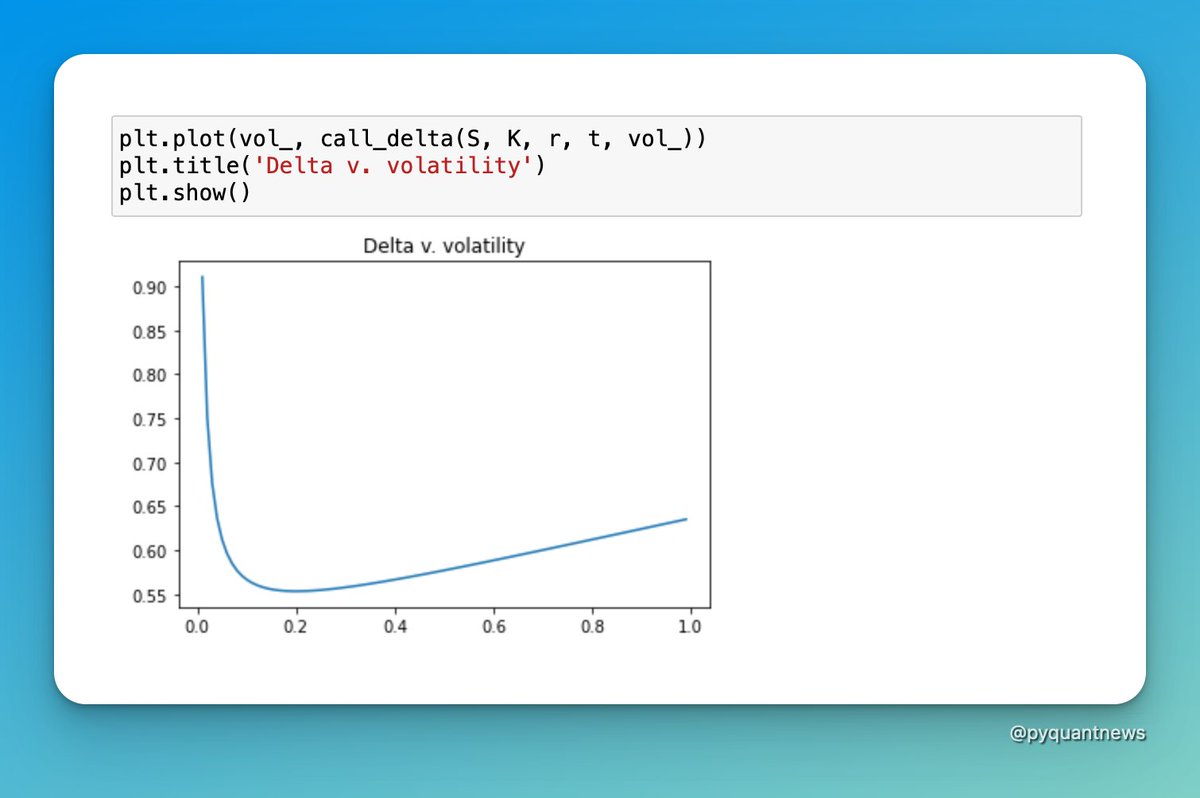
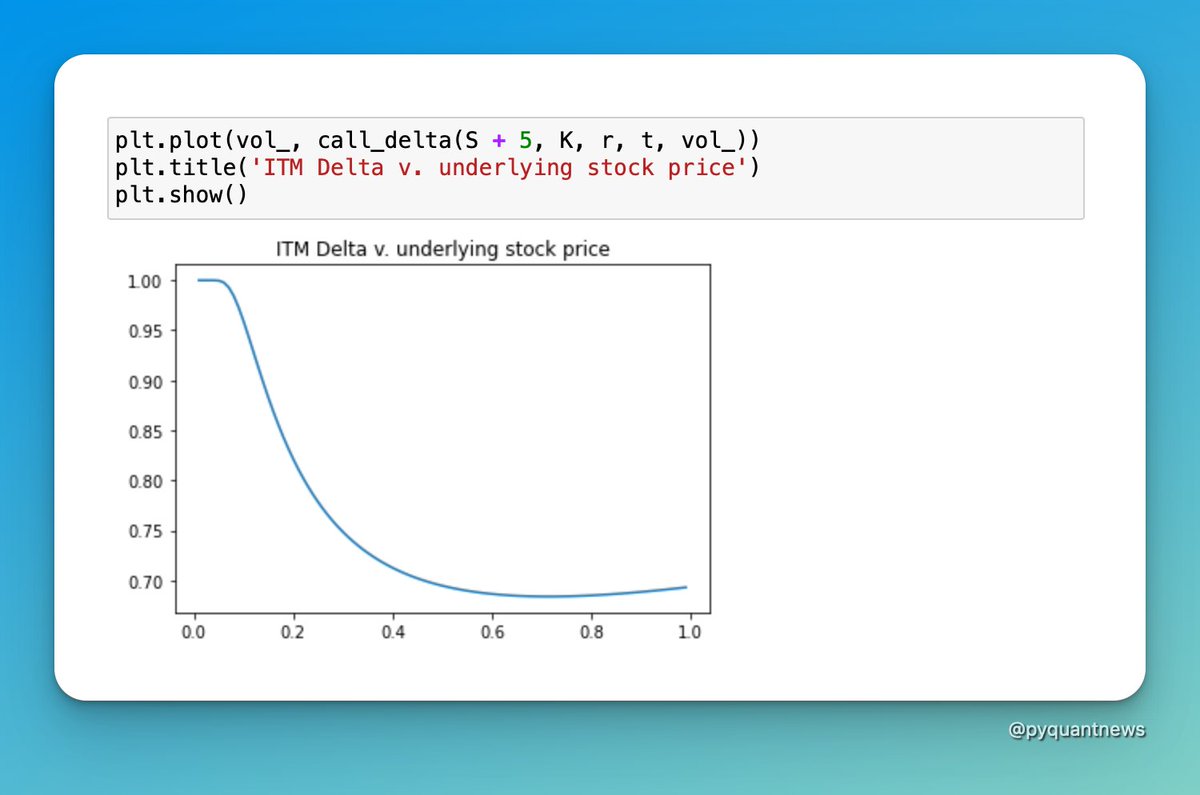
Weโre going to take a look at how delta behaves when the stock price, time to expiry, and volatility change.
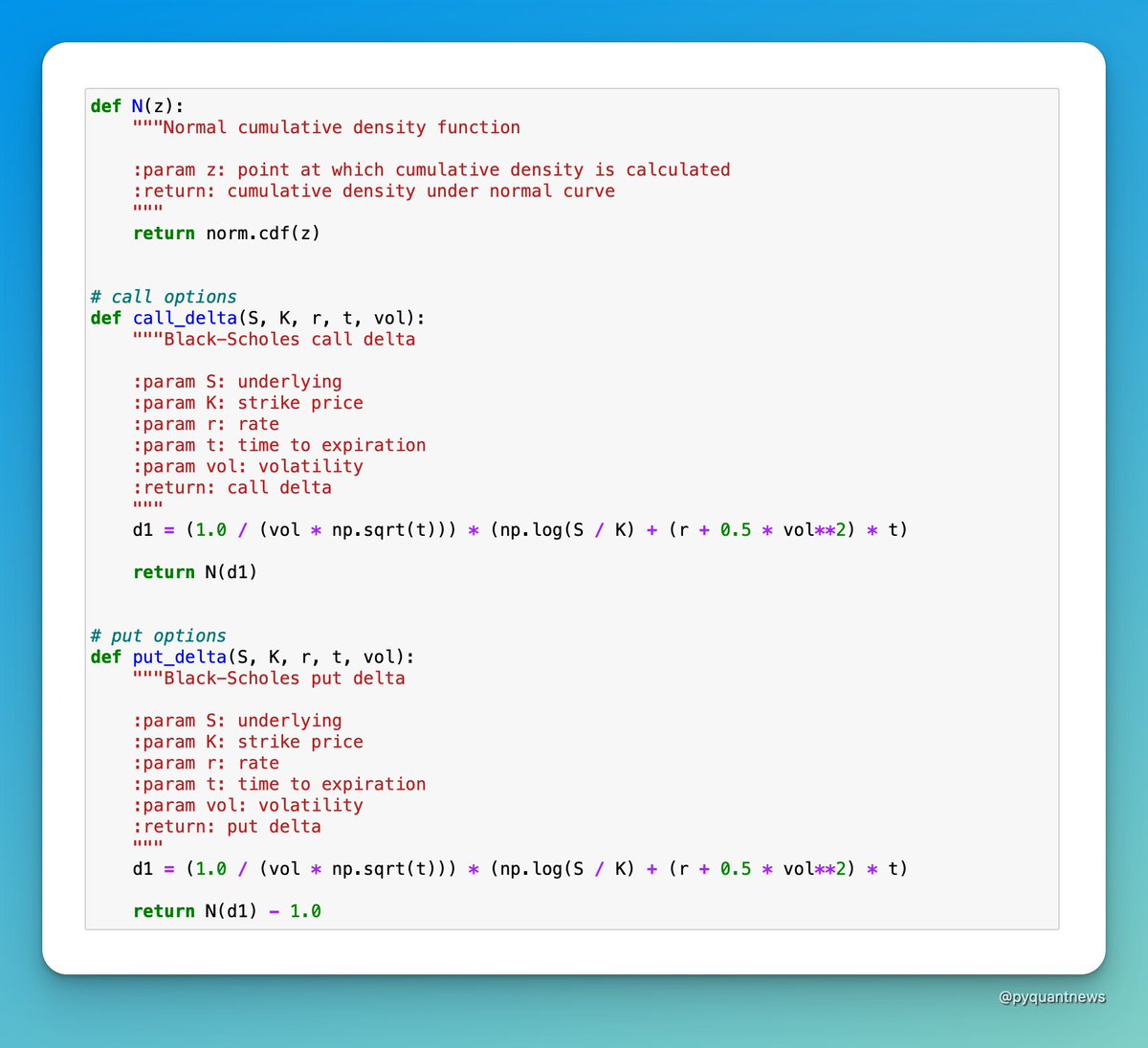
I'll use the Black-Scholes delta to demonstrate.
(If you want to learn more about Black-Scholes, you might be interested in this thread.)
Letโs get started!
I'll use the Black-Scholes delta to demonstrate.
(If you want to learn more about Black-Scholes, you might be interested in this thread.)
Letโs get started!
I start by defining the variables I need to calculate the delta:
โข Volatility
โข Stock price
โข Strike price
โข Interest rate
โข Time to expiration
The function is "vectorized" so passing an array of values returns an array of deltas.
This is useful for creating the charts.
โข Volatility
โข Stock price
โข Strike price
โข Interest rate
โข Time to expiration
The function is "vectorized" so passing an array of values returns an array of deltas.
This is useful for creating the charts.
The functions for call and put delta are straightforward in Python.
I use โat-the-moneyโ (ATM) call options for the analysis.
That means the stock price and strike price are equal.
("In-the-money" means the stock price is greater than the strike for calls - opposite for puts.)
I use โat-the-moneyโ (ATM) call options for the analysis.
That means the stock price and strike price are equal.
("In-the-money" means the stock price is greater than the strike for calls - opposite for puts.)
What happens to the delta as the underlying stock price increases?
The delta increases - which makes sense.
The further the stock price is ITM, the more likely it is to stay ITM at expiration.
At expiration, an ITM option is worth something - an OTM option is worth nothing.
The delta increases - which makes sense.
The further the stock price is ITM, the more likely it is to stay ITM at expiration.
At expiration, an ITM option is worth something - an OTM option is worth nothing.
How about when the expiration increases?
For ATM options, delta approaches 1.0 as the time to expiration increases.
The intuition?
The longer the option has before it expires, the more chance it has to expire ITM.
What about volatility?
For ATM options, delta approaches 1.0 as the time to expiration increases.
The intuition?
The longer the option has before it expires, the more chance it has to expire ITM.
What about volatility?
The higher the volatility of a stock, the more uncertainty about where the price will end up at expiration.
For ATM options, when volatility is very low, the delta is very high.
That's because the stock price doesn't move around a lot and a 1 cent move will put the option ITM.
For ATM options, when volatility is very low, the delta is very high.
That's because the stock price doesn't move around a lot and a 1 cent move will put the option ITM.
"Out-of-the-money" options have a delta near 0.0 when volatility is very low.
(Out-of-the-money (OTM) means the stock price is less than the strike price for calls - opposite for puts.)
If an option is OTM and there's no volatility, it's likely to expire worthless.
(Out-of-the-money (OTM) means the stock price is less than the strike price for calls - opposite for puts.)
If an option is OTM and there's no volatility, it's likely to expire worthless.
ITM options have a delta near 1.0 when volatility is very low.
Thatโs because if an option is ITM, and thereโs no volatility to move the stock around, itโs likely the option will expire ITM - and be worth something.
Thatโs because if an option is ITM, and thereโs no volatility to move the stock around, itโs likely the option will expire ITM - and be worth something.
This thread explored the relationship between delta, the stock price, time to expiration, and volatility.
There's more to delta, but to get started you need to know the intuition behind these relationships.
This thread gave you that intuition.
There's more to delta, but to get started you need to know the intuition behind these relationships.
This thread gave you that intuition.
To dive deeper, you may be interested in the Ultimate Guide to Pricing Options and Implied Volatility With Python:
Now with LIVE OPTIONS DATA.
Payoffs, Black-Scholes, Greeks, implied volatility, analysis.
All in a Jupyter Notebook you can run.
pyquantnews.gumroad.com
Now with LIVE OPTIONS DATA.
Payoffs, Black-Scholes, Greeks, implied volatility, analysis.
All in a Jupyter Notebook you can run.
pyquantnews.gumroad.com
Keep this thread handy as you continue to explore delta.
Hop back to the top and retweet the top tweet so you can find it later - and so others can find it too!
Here's the link:
Hop back to the top and retweet the top tweet so you can find it later - and so others can find it too!
Here's the link:
If you like Tweets like this, you might enjoy my weekly newsletter: The PyQuant Newsletter.
Join 4,000+ subscribers.
Python code for quantitative analysis you can use. Always 4 minutes or less.
pyquantnews.com
Join 4,000+ subscribers.
Python code for quantitative analysis you can use. Always 4 minutes or less.
pyquantnews.com
Loading suggestions...