1/7 Bias-variance tradeoff is probably the single most important concept in all of machine learning.
Thread: 🧵⬇️
Thread: 🧵⬇️
2/7 In statistical inference, Bias can be defined as the expectation of the difference between the actual parameters x from the estimated parameters x* ( Bias =E[x* -x] ) while Variance is simply the covariance between the estimated parameters x* ( Var =Cov(x*) )
3/7 In ML, given an estimator f' and the actual function f, Bias is the expectation of the difference between the estimator f' and the actual value f ( Bias = Ε[f' -f] ) while Variance is the covariance between different f' ( Var= E[f'] ) )
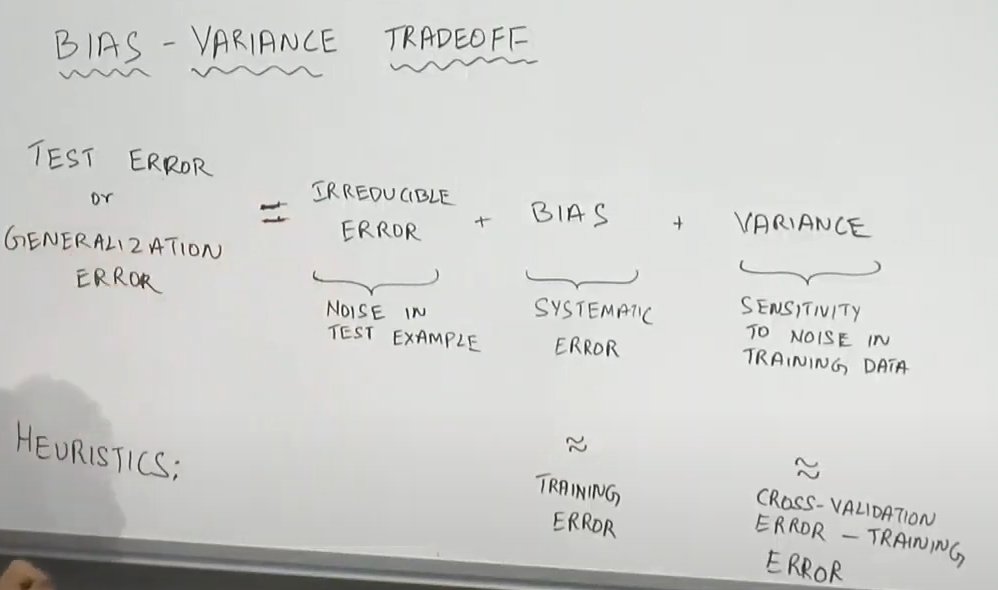
4/7 Bias is intuitively the systematic error of our estimator while Variance is the error from sensitivity to small fluctuations in the training set. In practice, we associate Bias with the Training error and Variance with the (Cross-validation error - Training Error)
5/7 Overfitting relates to having a High Variance estimator. It can be solved by increasing regularization, obtaining a larger data set, decreasing the number of features, or using a smaller model.
6/7 Underfitting relates to having a High Bias estimator. To fight underfitting, we can decrease regularization, use more features, use a larger model, etc
7/7 The bias–variance tradeoff is the conflict in trying to simultaneously minimize these two sources of error that prevent supervised learning algorithms from achieving a high generalization error.
Loading suggestions...