here's a real calculus moment - finding the closest point between a ray/line and a spline (thread)
• the spline is a function p(u) where u is the parameter/time value
• let's define a function f(u) that returns the squared distance between the ray and the spline
• let's define a function f(u) that returns the squared distance between the ray and the spline
first, we sample distance from some number of points across the spline, and find our initial guess for which one *seems* to be the value with the smallest distance
now, this isn't very accurate - but it's close to a local minima! remember how to find extrema from math class?
now, this isn't very accurate - but it's close to a local minima! remember how to find extrema from math class?
any extrema, will live where the slope (derivative, or, rate of change) changes sign
where it goes from sloping down, to up (local minima), or from up to down (local maxima)
this means, the points at extrema is where the derivative f'(u) = 0
where it goes from sloping down, to up (local minima), or from up to down (local maxima)
this means, the points at extrema is where the derivative f'(u) = 0
remember how to find out where a function is 0?
this is called root solving, where you usually pull out some formulas for your quadratic equations to find the roots
however, this function is way more complex than a simple quadratic polynomial :c
so, what do we do?
this is called root solving, where you usually pull out some formulas for your quadratic equations to find the roots
however, this function is way more complex than a simple quadratic polynomial :c
so, what do we do?
we use a numeric method!
one such method is the newton-rhapson method, where you start with an initial guess, and iteratively refine the search several times
it's actually pretty simple! given an initial guess of x, the new value of x is:
x - f(x)/f'(x)
one such method is the newton-rhapson method, where you start with an initial guess, and iteratively refine the search several times
it's actually pretty simple! given an initial guess of x, the new value of x is:
x - f(x)/f'(x)
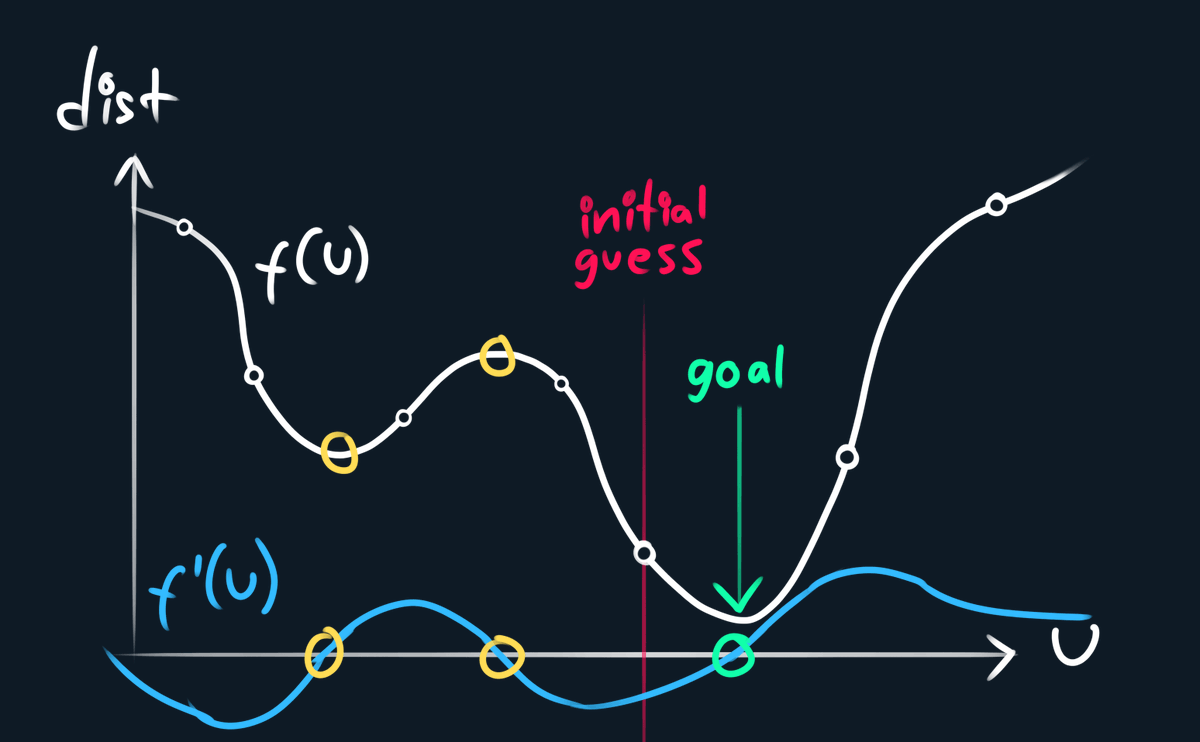
now remember, we don't want to find the roots of the distance function (where distance is 0), but rather the root of the *derivative* of the distance function (where distance is at a local extrema)
so, all we need is a few iterations of this:
u = u - f'(u)/f''(u)
so, all we need is a few iterations of this:
u = u - f'(u)/f''(u)
now, we need both the 1st and the 2nd derivative of our distance function, which is actually pretty non-trivial, even if our spline is easily differentiable
but uh it's doable
f(u) is the squared distance function
p(u) is the spline function
o is the ray origin
n is the ray dir
but uh it's doable
f(u) is the squared distance function
p(u) is the spline function
o is the ray origin
n is the ray dir
anyway that's it! the cool thing about this method is that it actually converges very quickly, the .gif up top has 4 initial guesses per curve segment, and just 4 newton-rhapson iterations 🎉
also newton-rhapson is perfectly stable there ar eno edge casess there's nothing to worryr about just don't read wuiipkipedia it's fine everythings fine jsut don't read wik
here's the distance function and its derivative visualized!
Loading suggestions...