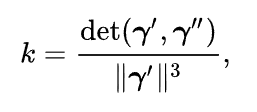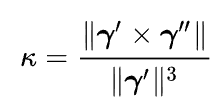curvature is a bivector right?
it seems to be
f'(x) ∧ f''(x) divided by ||f'(x)||^3
right?
in 2D, it's the determinant, and in 3D it's the cross product, so it smells like a bivector situation to me, and it makes intuitive sense as well
f'(x) ∧ f''(x) divided by ||f'(x)||^3
right?
in 2D, it's the determinant, and in 3D it's the cross product, so it smells like a bivector situation to me, and it makes intuitive sense as well
like, remove the magnitude of the numerator in the 3D version, and it returns the usual pseudovector "axis of rotation", when I think in reality it's just a bivector we interpret as if it's a vector
this would also help explain why curvature is a scalar with a sign in 2D, but in 3D it "doesn't have a sign", or rather, it's not supposed to be a scalar, or a vector, it's a bivector!
like I'm pretty sure this is the case but I haven't verified it
like I'm pretty sure this is the case but I haven't verified it
Loading suggestions...