(1/25) Cryptography Fundamentals: Elliptic Curve Cryptography
Elliptic Curve Cryptography is (one of) our strongest cryptographic tools, vastly more secure than its predecessors. But... how does the moon math at the center of modern crypto work?
A layman's guide to Sci-Fi tech
Elliptic Curve Cryptography is (one of) our strongest cryptographic tools, vastly more secure than its predecessors. But... how does the moon math at the center of modern crypto work?
A layman's guide to Sci-Fi tech
(2/25) The internet is a very public place. It basically works by blasting information at anyone listening, hoping itโll get to its intended recipient.
Need to send a private message? Someone else WILL get a copy of the data; youโre going to need a cryptographic algorithm.
Need to send a private message? Someone else WILL get a copy of the data; youโre going to need a cryptographic algorithm.
(3/25) A cryptographic algorithm receives a message and an encryption key.
If the message is not encrypted, the algorithm will transform it into illegible nonsense, securing the data.
If the message is encrypted (and the key matches the encoding), the algorithm will decode it.
If the message is not encrypted, the algorithm will transform it into illegible nonsense, securing the data.
If the message is encrypted (and the key matches the encoding), the algorithm will decode it.
(4/25) Just treat encryption algorithms like a black box, letโs focus on the encryption keys.
Anyone that has a copy has access to your messages, so we need to ensure it stays secret between you and whoever youโre talking to.
Soโฆ how do we create a shared secret in public?
Anyone that has a copy has access to your messages, so we need to ensure it stays secret between you and whoever youโre talking to.
Soโฆ how do we create a shared secret in public?
(5/25) The first answer is Diffie-Hellman Key Exchange, a process that allows two entities to privately generate a shared secret by sharing public information.
(From here on thereโs math, but itโs easy. You do need to know modular arithmetic, covered in the linked thread).
(From here on thereโs math, but itโs easy. You do need to know modular arithmetic, covered in the linked thread).
(6/25) The crux of Diffie-Hellman is in the equation below - specifically in how incredibly difficult it is to undo.
The problem with modular arithmetic is itโs very difficult to figure out how many times the value looped through the maximum.
The problem with modular arithmetic is itโs very difficult to figure out how many times the value looped through the maximum.
(7/25) Letโs say you are listening to a Diffie-Hellman exchange. You are able to learn:
n = 23
g = 5
g^a mod n = 4
We know g^a has a remainder of 4โฆ thatโs not enough info. Does g^a = 27? 50? 73? There are literally infinite options.
n = 23
g = 5
g^a mod n = 4
We know g^a has a remainder of 4โฆ thatโs not enough info. Does g^a = 27? 50? 73? There are literally infinite options.
(8/25) One way to do it is to just start guessing. Quickly youโll realize that a = 4. But with sufficiently large numbers, this can take forever.
Computation in one direction is easy, but undoing it is super difficult. We call these types of functions Trapdoor Functions.
Computation in one direction is easy, but undoing it is super difficult. We call these types of functions Trapdoor Functions.
(9/25) Trapdoor functions form the basis of strong encryption.
First Diffie-Hellman built a protocol around modular arithmetic.
Next, RSA extended on these ideas to build around factoring large numbers.
Unfortunately, we are starting to get better and better at solving both.
First Diffie-Hellman built a protocol around modular arithmetic.
Next, RSA extended on these ideas to build around factoring large numbers.
Unfortunately, we are starting to get better and better at solving both.
(10/25) In summary, this is the world we find ourselves in:
1) cryptography is about creating shared secrets using public channels
2) a trapdoor function provides the foundation for cryptographic security
3) we are getting to good at solving the old trapdoor functions
1) cryptography is about creating shared secrets using public channels
2) a trapdoor function provides the foundation for cryptographic security
3) we are getting to good at solving the old trapdoor functions
(11/25) This is where elliptic curve cryptography comes into play. The elliptic curve provides the context needed for a (much) better trapdoor function.
We begin with an elliptic curve, defined below.
We begin with an elliptic curve, defined below.
(12/25) We will define the dot operation to take advantage of the curveโs unique shape and horizontal symmetry.
Shape: a line drawn through 2 points will intersect with the curve once (and only once) more
Symmetry: the curve always exists in the same place opposite the x-axis.
Shape: a line drawn through 2 points will intersect with the curve once (and only once) more
Symmetry: the curve always exists in the same place opposite the x-axis.
(13/25) If youโre paying close enough attention, you can already see the trapdoor function begin to form
Need a hint? Modular arithmetic was difficult to undo because you canโt tell how many times the value looped over the maximum (n). 1 iteration is indistinguishable from 1000
Need a hint? Modular arithmetic was difficult to undo because you canโt tell how many times the value looped over the maximum (n). 1 iteration is indistinguishable from 1000
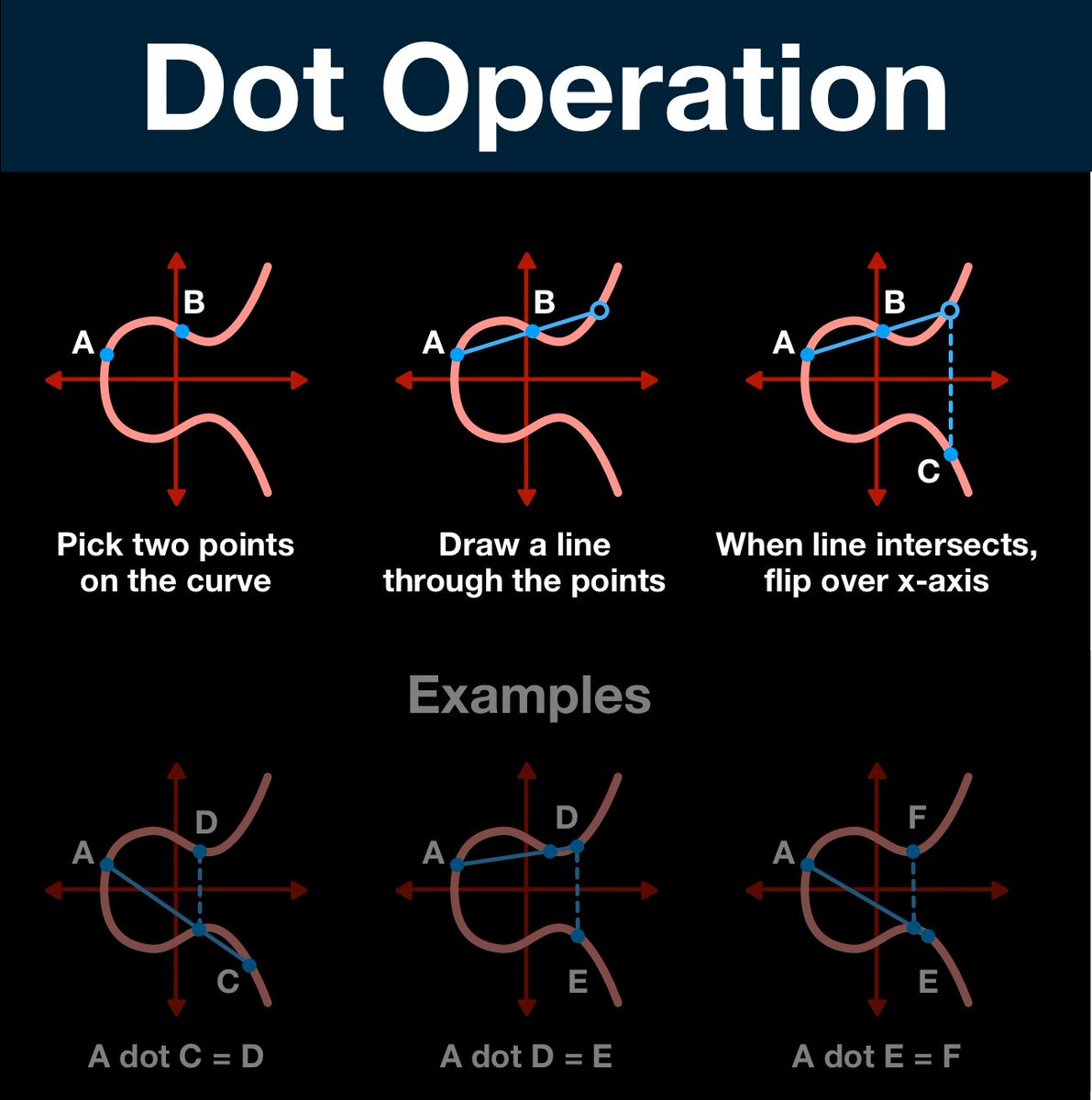
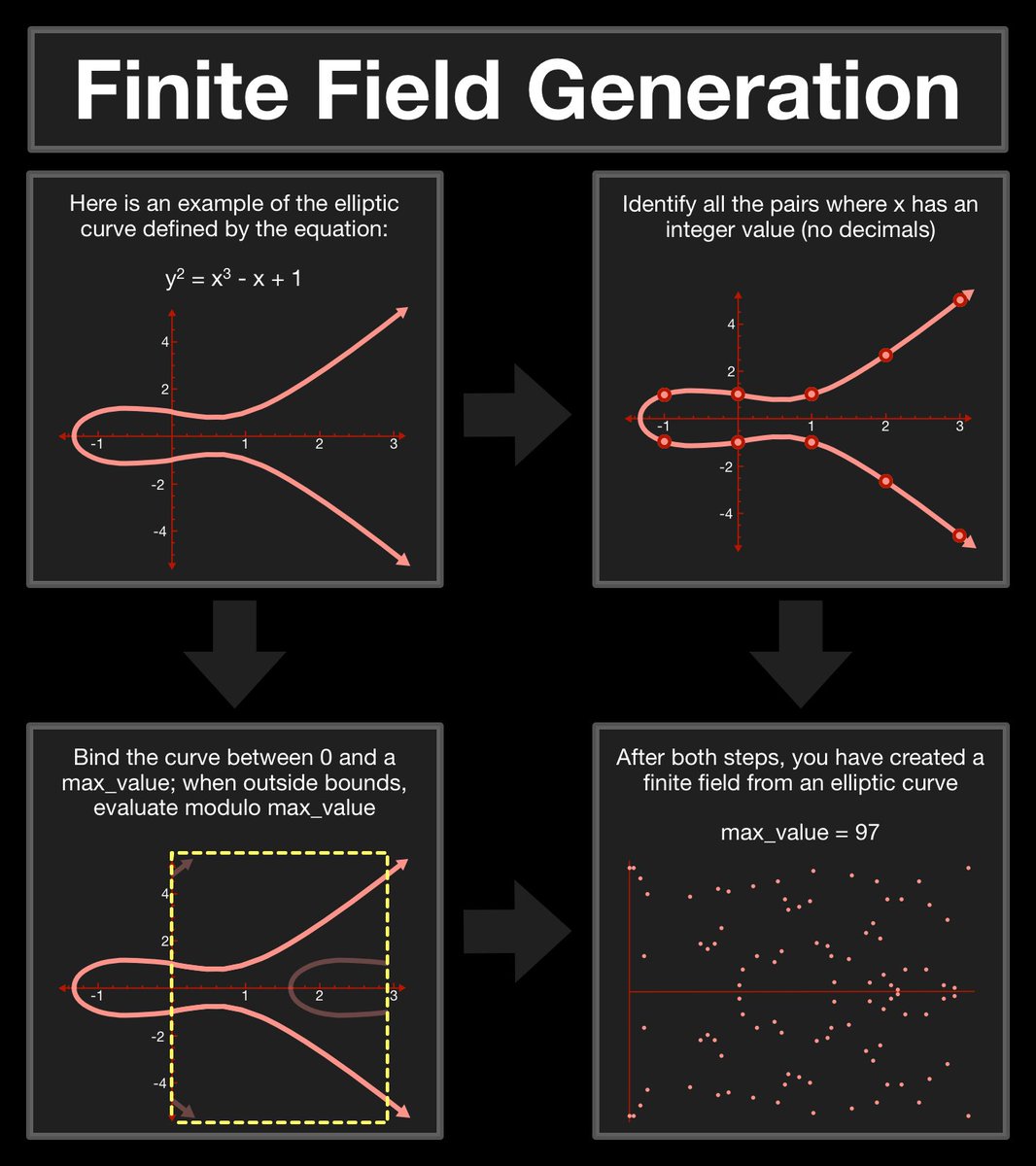
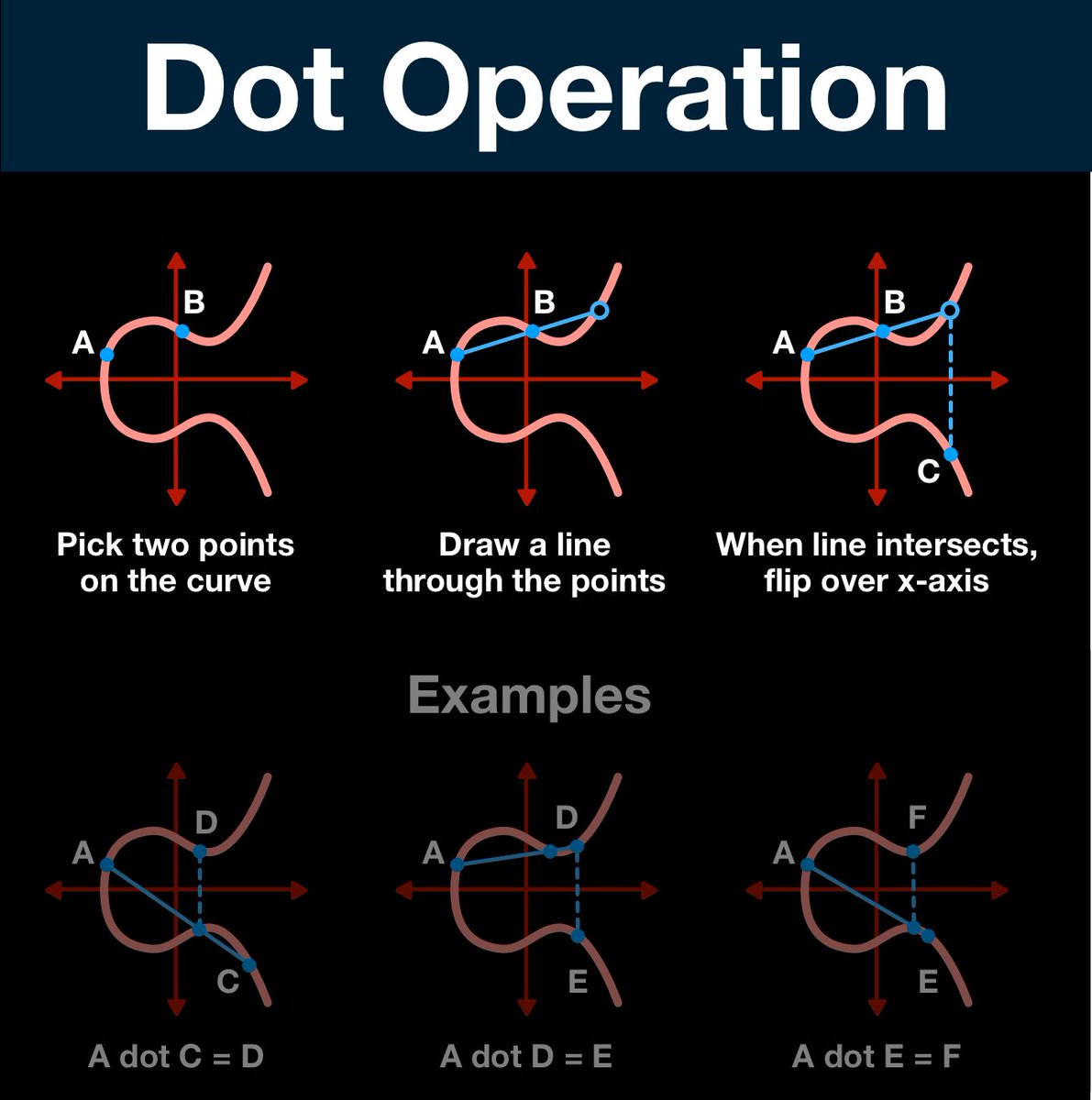
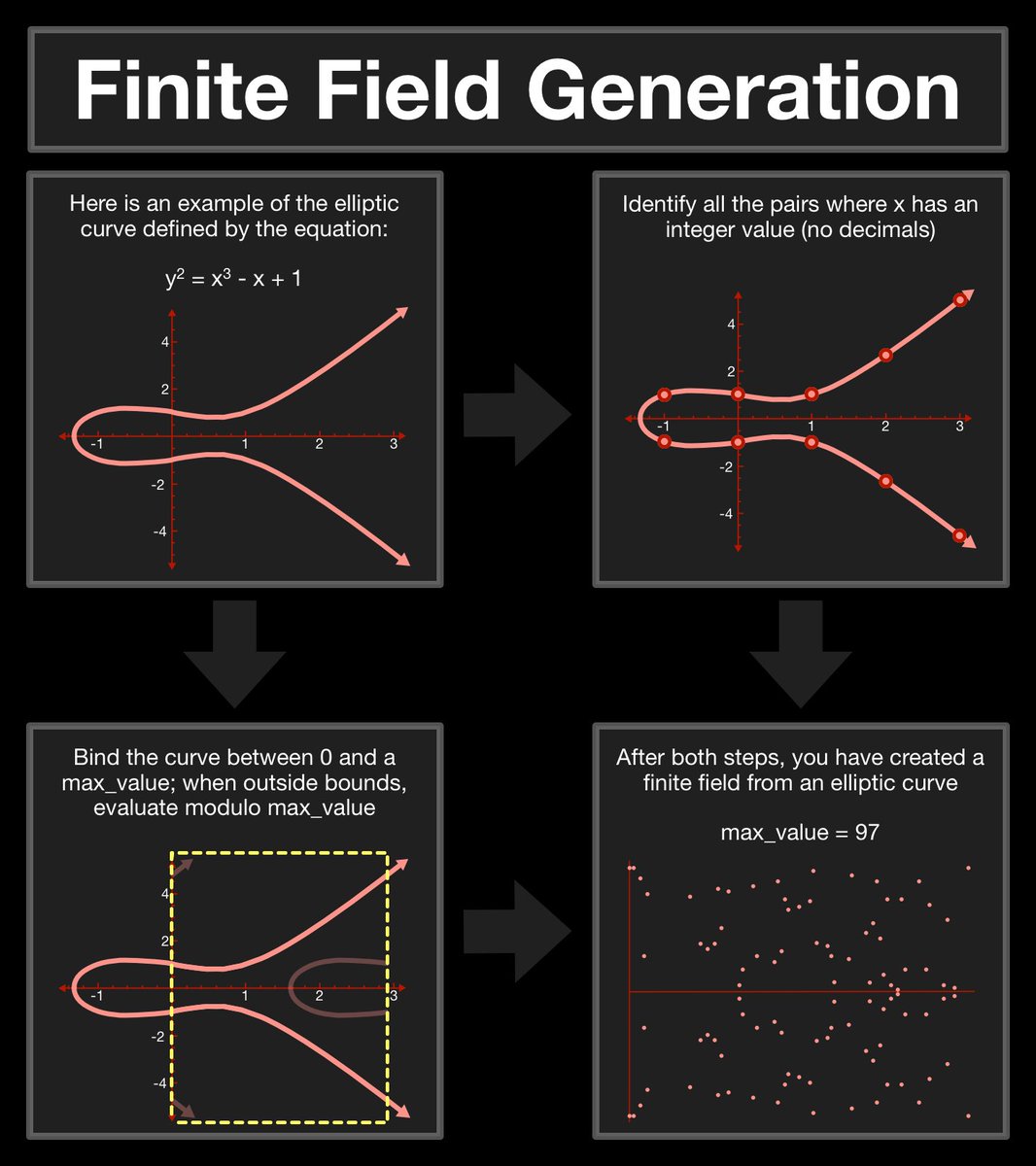
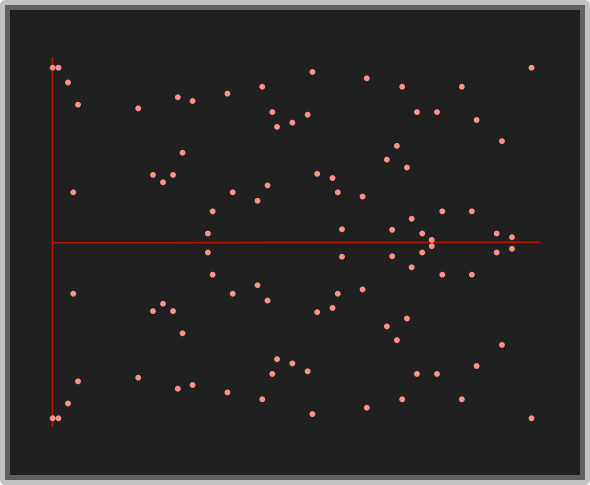
(14/25) This is what we are going to build out of the dot operation, but first we need to prepare our workspace.
In its current state, an elliptic curve is much to infinite. How many values exist between x = 1 and x = 2? How big can the values get?
In its current state, an elliptic curve is much to infinite. How many values exist between x = 1 and x = 2? How big can the values get?
(15/25) We are going to apply two operations to our curve:
- ignore all values where x has a decimal (whole integers only)
- create max and min boundaries around the curve, folding over any parts that fall outside (similar to modular arithmetic)
- ignore all values where x has a decimal (whole integers only)
- create max and min boundaries around the curve, folding over any parts that fall outside (similar to modular arithmetic)
(16/25) The discrete field still retains the properties required to implement the dot operation.
Most importantly, the field retains horizontal symmetry (symmetry across the x-axis). Take a look:
Most importantly, the field retains horizontal symmetry (symmetry across the x-axis). Take a look:
(17/25) In fact, dot operations in these finite fields are nearly identical to dot operations in elliptical curves
Each dot operation creates a line between two points, continuing until it intersects one more point. Then just flip across the x-axis and find the symmetrical point
Each dot operation creates a line between two points, continuing until it intersects one more point. Then just flip across the x-axis and find the symmetrical point
(18/25) During the dot operation, if our line moves outside the bounds we've set, we simply wrap the line around.
Did you ever play the game Asteroids? Same idea: if you move off the screen you just reappear on the other side with the same trajectory.
Did you ever play the game Asteroids? Same idea: if you move off the screen you just reappear on the other side with the same trajectory.
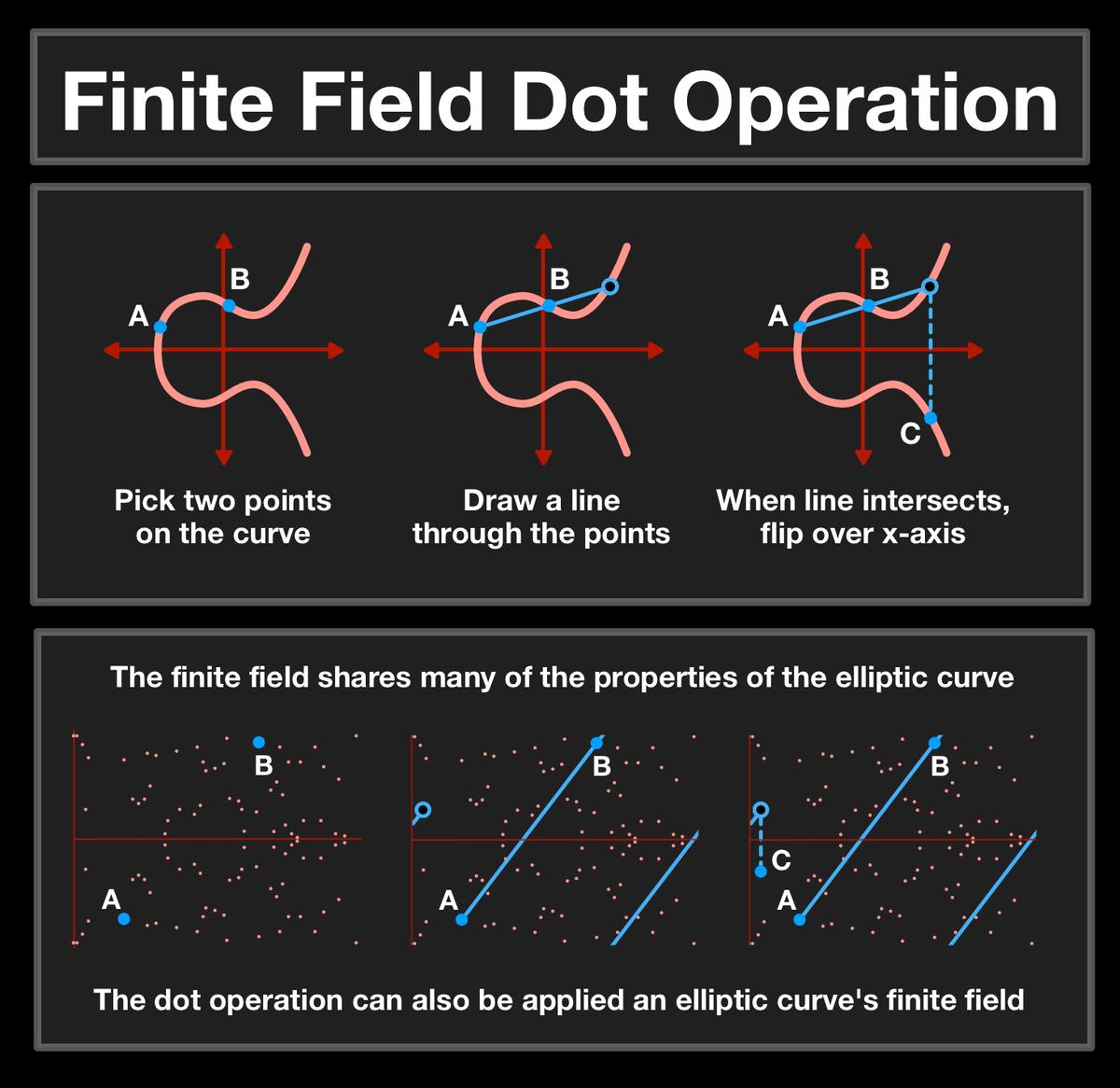
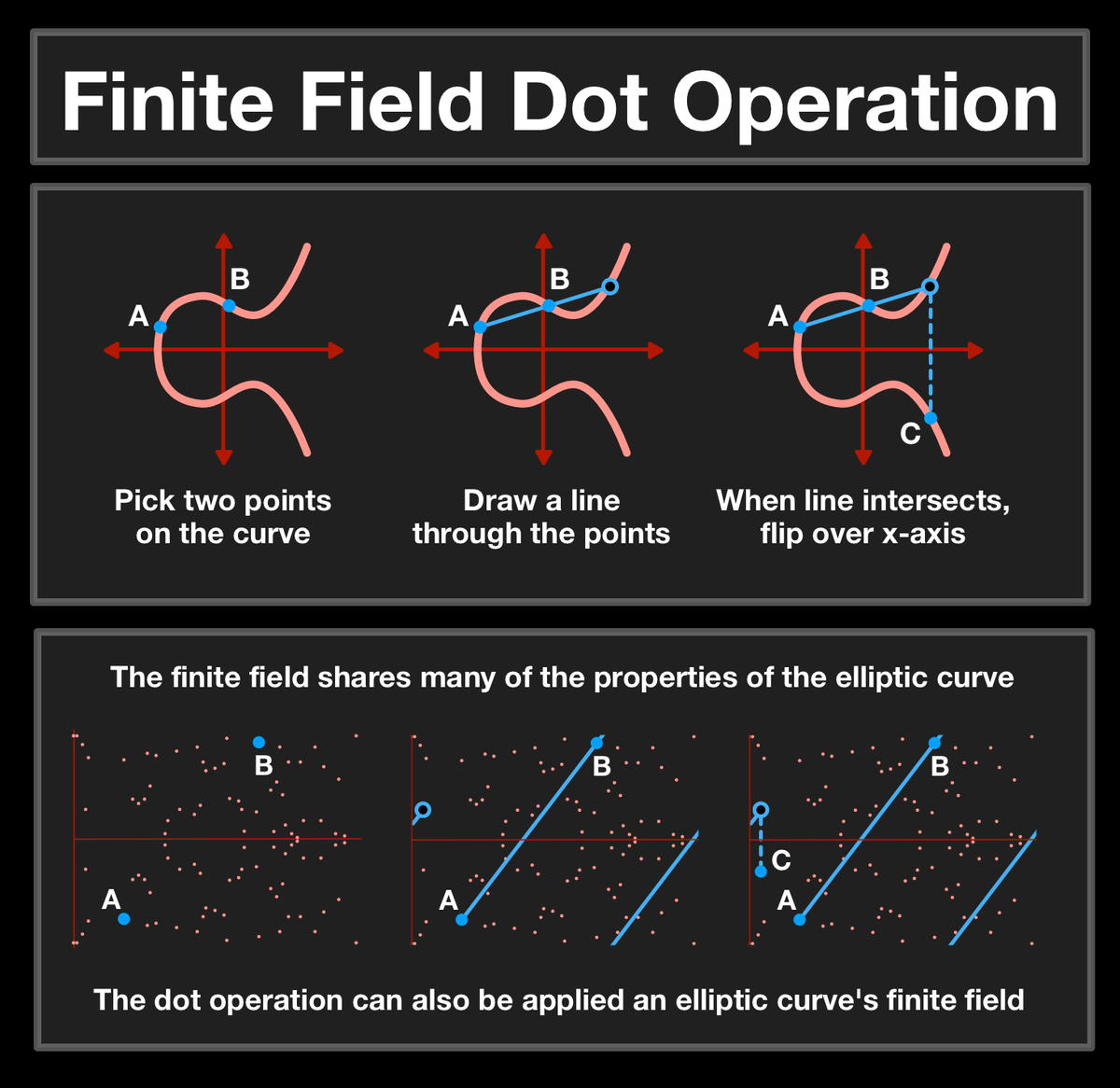
(19/25) Computing the number of times a point was dotted is a process called the elliptic curve discrete logarithm function; turns out that the function is INCREDIBLY hard to solve.
In fact, there isn't a better method than just guessing and checking.
In fact, there isn't a better method than just guessing and checking.
(20/25) Just like a Diffie-Hellman system, we can build a system based on the elliptic curve that uses this one-way function to create a shared secret.
Diffie-Hellman uses a prime maximum (n), a base public base (g) and a private key (a or b) to generate a shared secret.
Diffie-Hellman uses a prime maximum (n), a base public base (g) and a private key (a or b) to generate a shared secret.
(21/25) An elliptic curve system is (can be) defined by picking a prime number as a max, a curve equation and a public point on the curve.
A private key is a number PRIV, and a public key is the public point dotted with itself PRIV times.
A private key is a number PRIV, and a public key is the public point dotted with itself PRIV times.
(22/25) When comparing elliptic curve and Diffie-Hellman (and RSA) cryptography, we must compare trapdoor functions.
We've made progress on factoring, improving our solving process and increasing computing power. Diffie-Hellman (and RSA) are becoming less and less secure.
We've made progress on factoring, improving our solving process and increasing computing power. Diffie-Hellman (and RSA) are becoming less and less secure.
(23/25) Elliptic curve discrete logarithm function? It's been ~30 years and STILL no one has anything better than guessing.
The result: for numbers of the same size, solving elliptic curve discrete logarithms is significantly harder than factoring.
The result: for numbers of the same size, solving elliptic curve discrete logarithms is significantly harder than factoring.
(24/25) Arjen Lenstra framed it best in Universal Security
Tl;dr breaking a 228-bit RSA key requires less energy to than it takes to boil a teaspoon of water. Breaking a 228-bit elliptic curve key requires enough energy to boil all the water on earth.
eprint.iacr.org
Tl;dr breaking a 228-bit RSA key requires less energy to than it takes to boil a teaspoon of water. Breaking a 228-bit elliptic curve key requires enough energy to boil all the water on earth.
eprint.iacr.org
(25/25) Cryptography is the quest to transfer private data through public channels. Alas, we live in a human world; humans inevitably try to break into secrets
First, Diffie and Hellman (& Merkle) gave us a tool; one that's aging (quickly)
Fortunately, we have elliptic curves!
First, Diffie and Hellman (& Merkle) gave us a tool; one that's aging (quickly)
Fortunately, we have elliptic curves!
Like what you read? Help me spread the word by retweeting the thread (linked below).
Follow me for more explainers and as much alpha as I can possibly serve.
Follow me for more explainers and as much alpha as I can possibly serve.
Loading suggestions...