(1/18) Cryptography Basics: Polynomial Encoding
Humans think in words and ideas, machines think in numbers and math; the translation of words into numbers is core to basic computing.
Want to learn about the powers we have in this process? Let's start with Lagrange Polynomials.
Humans think in words and ideas, machines think in numbers and math; the translation of words into numbers is core to basic computing.
Want to learn about the powers we have in this process? Let's start with Lagrange Polynomials.
(2/18) Preface:
This is part of a series on elliptic curve cryptography and its applications for @ethereum. This is simplified to a MINIMAL level, aiming at ~high-school math.
@VitalikButerin @dankrad @danboneh @chaseklvk, if you read this, I'm sorry for what I did to the math.
This is part of a series on elliptic curve cryptography and its applications for @ethereum. This is simplified to a MINIMAL level, aiming at ~high-school math.
@VitalikButerin @dankrad @danboneh @chaseklvk, if you read this, I'm sorry for what I did to the math.
(3/18) Quick refresher: polynomials
A polynomial is an equation made up of one or more groups of terms that are combined together with addition or subtraction.
This is just the basic stuff you remember from high school math.
mathsisfun.com
A polynomial is an equation made up of one or more groups of terms that are combined together with addition or subtraction.
This is just the basic stuff you remember from high school math.
mathsisfun.com
(4/18) Normally you would see a polynomial written in function form (as seen below).
The f(x) notation can be read as "x is a placeholder in this function. When I am ready to evaluate it, replace x with the evaluation number and calculate the result."
The f(x) notation can be read as "x is a placeholder in this function. When I am ready to evaluate it, replace x with the evaluation number and calculate the result."
(5/18) A function can generate an infinite number of points; you control the input (x) and so you can just keep changing it to produce more and more outputs.
And so, a function is an incredibly efficient way to express data. One line can represent infinite points.
And so, a function is an incredibly efficient way to express data. One line can represent infinite points.
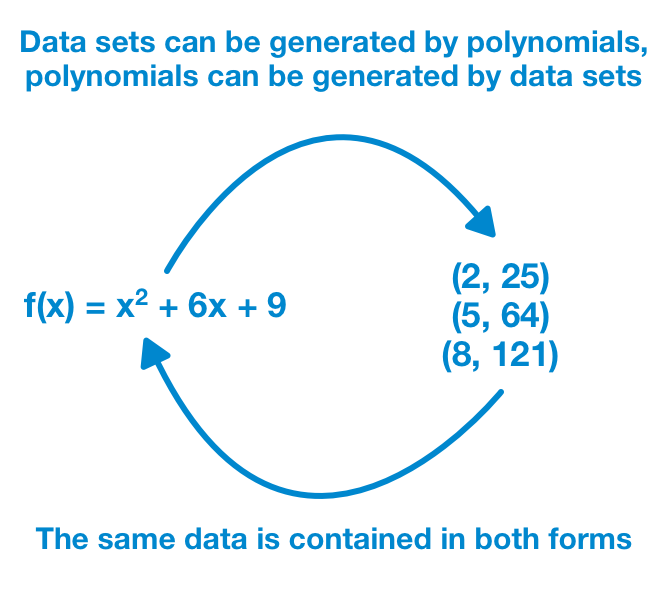
(6/18) So, here's a question: if a function can represent a huge amount of data in one expression, can we go backward? Can you take a huge amount of data and create a representative single expression?
The answer, of course, is yes! And we've know how for over 200 years!
The answer, of course, is yes! And we've know how for over 200 years!
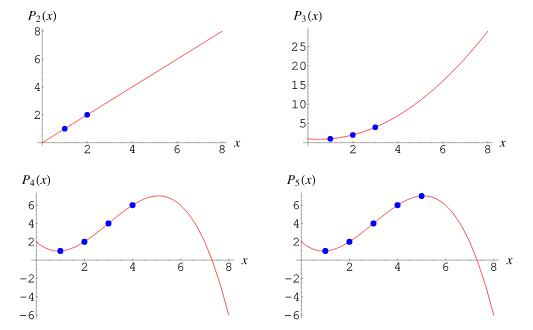
(7/18) A Lagrange polynomial the simplest, unique polynomial that fits a particular set of data (simplest meaning it has the least possible polynomial terms -- lowest possible degree).
Frankly, the math is absurd; we will take it for granted.
en.wikipedia.org
Frankly, the math is absurd; we will take it for granted.
en.wikipedia.org
(8/18) Regardless of how wild your data is, there exists a line that passes through all of it.
All you really need to know about a Lagrange polynomial that is is the simplest function that will evaluate to all of your points.
And that it's (relatively) easy/quick to compute.
All you really need to know about a Lagrange polynomial that is is the simplest function that will evaluate to all of your points.
And that it's (relatively) easy/quick to compute.
(9/18) Let's just assume that it's actually so quick and easy to commute that it is entirely irrelevant to modern computing. That we can basically consider a function and a set of evaluation points equivalent.
(10/18) Let's take a step away from polynomials for a moment; I want you to think about computer data.
For example, let's take a look at a single world: STUART. These 6 letters are displayed to you, but that's not how your computer understands them.
For example, let's take a look at a single world: STUART. These 6 letters are displayed to you, but that's not how your computer understands them.
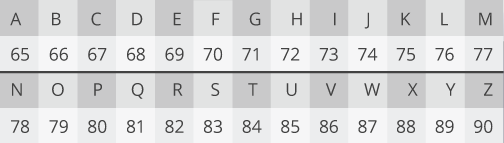
(11/18) Your computer thinks in numbers and math, and so must represent STUART numerically. Behind the scenes, each letter is represented by a number. The number is stored by the computer, it is only changed to a letter for human eyes.
(12/18) Here is an encoding table for the Latin alphabet. Every letter has a unique number; a computer will store and process the numerical version, a human will be able to work with the letter version.
And so, STUART is 83, 84, 85, 65, 82, 84
And so, STUART is 83, 84, 85, 65, 82, 84
(13/18) Using this method, we can convert any data into an ordered list of numbers.
If this doesn't make sense, stop here and shoot me a DM. This is critical: all data can be represented as a list of numbers.
If you're still here with me, you've gotten to the magic part...
If this doesn't make sense, stop here and shoot me a DM. This is critical: all data can be represented as a list of numbers.
If you're still here with me, you've gotten to the magic part...
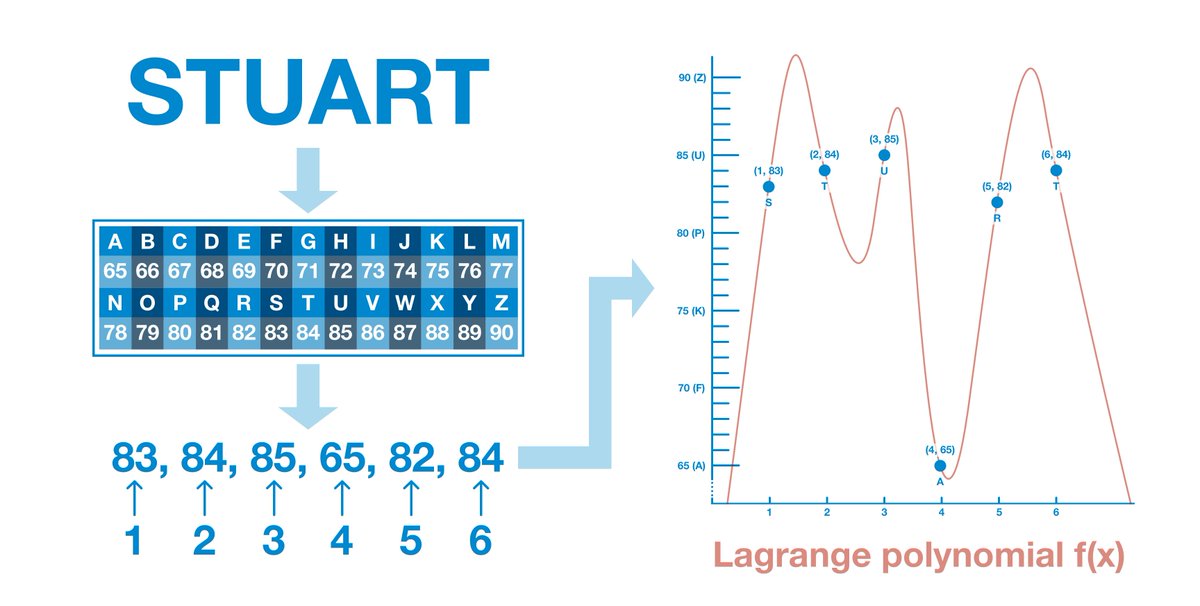
(14/18) STUART = 83, 84, 85, 65, 82, 84. Put another way:
- First position: 83
- Second position: 84
- Third position: 85
- Fourth position: 65
- Fifth position: 82
- Sixth position: 84
How about we just write it like this:
1, 83
2, 84
3, 85
4, 65
5, 82
6, 84
- First position: 83
- Second position: 84
- Third position: 85
- Fourth position: 65
- Fifth position: 82
- Sixth position: 84
How about we just write it like this:
1, 83
2, 84
3, 85
4, 65
5, 82
6, 84
(15/18) In fact, you can transform any data into a set of points of an x,y graph by breaking the data into pieces.
X: the piece number
Y: the specific data at that piece number
Once you have a set of points, you can derive the Lagrange polynomial.
X: the piece number
Y: the specific data at that piece number
Once you have a set of points, you can derive the Lagrange polynomial.
(16/18) Let me reiterate for you visual learners. Take your data (converted into numbers, broken into chunks) and add it to a graph, one chunk at a time.
When all the data is graphed, "draw" the polynomial through it to derive a single formula that expresses every data point.
When all the data is graphed, "draw" the polynomial through it to derive a single formula that expresses every data point.
(17/18) This is what we are here to learn:
1) it is possible to represent an arbitrary set of data as a polynomial
2) you can (relatively) quickly and easily find the equation of said polynomial through a process known as the Lagrange Interpolation
1) it is possible to represent an arbitrary set of data as a polynomial
2) you can (relatively) quickly and easily find the equation of said polynomial through a process known as the Lagrange Interpolation
(18/18) As we continue forward, we will learn why this is a useful property.
For now, just remember the big picture we covered in this thread:
Data → polynomial → data
Data = polynomial
For now, just remember the big picture we covered in this thread:
Data → polynomial → data
Data = polynomial
Like what you read? Help me spread the word by retweeting the thread (linked below).
Follow me for more explainers and as much alpha as I can possibly serve.
Follow me for more explainers and as much alpha as I can possibly serve.
Loading suggestions...