(1/13) KZG Commitments Part 2: Open
Previously, we committed to our data by evaluating a polynomial using an elliptic curve. Now, it's time to test that commitment; it's time for the verifier to see if the prover knows a specific piece of data.
It's time to open the commitment.
Previously, we committed to our data by evaluating a polynomial using an elliptic curve. Now, it's time to test that commitment; it's time for the verifier to see if the prover knows a specific piece of data.
It's time to open the commitment.
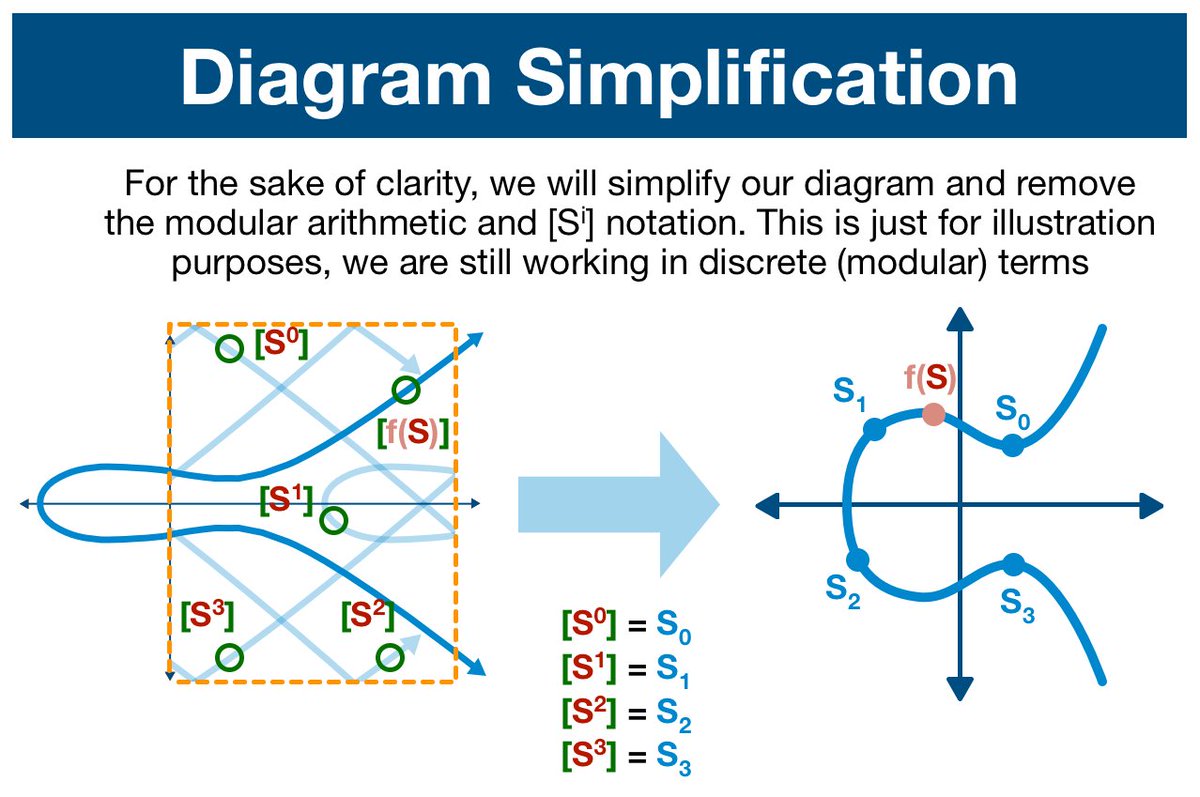
(2/13) The deeper we go, the more we are forced to simplify. Nevertheless, let's solider on!
All you need is high-school math and a willingness to read the images and linked tweets.
All you need is high-school math and a willingness to read the images and linked tweets.
(3/13) A polynomial commitment scheme allows one party to publicly commit to a specific dataset without giving away any info about the underlying data.
Once a commitment has been calculated, the data is locked in; any changes to the data will result in invalid proof generation.
Once a commitment has been calculated, the data is locked in; any changes to the data will result in invalid proof generation.
(4/13) A KZG polynomial commit can be "opened" with any data point without revealing the entire dataset.
Let's say I am thinking of 10 words. I write them each down on different pieces of paper. If you guess correct, i ONLY show you the correct 1 (keeping the other 9 hidden).
Let's say I am thinking of 10 words. I write them each down on different pieces of paper. If you guess correct, i ONLY show you the correct 1 (keeping the other 9 hidden).
(5/13) First, we generate a polynomial from our data using a mathematical process called a Lagrange Interpolation.
Then, we calculate the value of this polynomial evaluated with a secret number S (hidden within an elliptic curve).
Then, we calculate the value of this polynomial evaluated with a secret number S (hidden within an elliptic curve).
(6/13) Once the commitment is calculated, the prover is bound to this specific data. The scheme is going to pivot around this specific value, derived from this specific polynomial.
A change to even a single bit will result in a brand new polynomial (and therefore commit value).
A change to even a single bit will result in a brand new polynomial (and therefore commit value).
(7/13) < PAUSE >
At this point our graphic has become too cluttered to be useful, so we will simplify in the name of readability. Nothing has changed, we are still working in modular arithmetic.
< RESUME >
At this point our graphic has become too cluttered to be useful, so we will simplify in the name of readability. Nothing has changed, we are still working in modular arithmetic.
< RESUME >
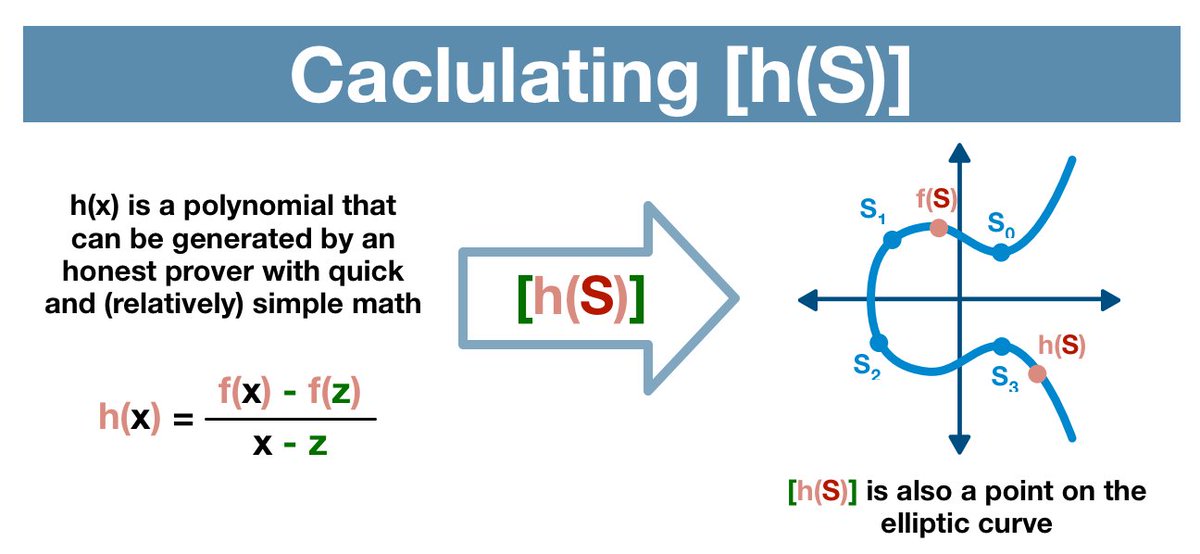
(8/13) Now that the prover has been bound to this specific set of data, we can test the commitment by opening a proof at singular piece of data.
The verifier, an independent entity who may or may not have access to the entire dataset, now chooses a piece of data to verify.
The verifier, an independent entity who may or may not have access to the entire dataset, now chooses a piece of data to verify.
(9/13) Let z be the piece of data the verifier is going to test... and so he sends z over to the prover.
First, the prover calculates f(z). This is very easy for the prover; he has already built the polynomial in order to generate the commitment. He simply runs z through.
First, the prover calculates f(z). This is very easy for the prover; he has already built the polynomial in order to generate the commitment. He simply runs z through.
(10/13) < Second wall break to paper over some math >
tl;dr you can divide polynomials. It's not a particularly complicated operation, in fact it (can) look like long division.
cuemath.com
< Back to the thread >
tl;dr you can divide polynomials. It's not a particularly complicated operation, in fact it (can) look like long division.
cuemath.com
< Back to the thread >
(11/13) Because the prover has built the polynomial, it is very easy for them to create the new polynomial h(x). h(x) is the quotient polynomial built off of our proof data z.
(12/13) This is it one more time, as simplified as possible.
The important takeaway: the verifier provides a value (a piece of data in the dataset to which the prover is committed) around which the prover is going to create an elliptic curve point and one other value.
The important takeaway: the verifier provides a value (a piece of data in the dataset to which the prover is committed) around which the prover is going to create an elliptic curve point and one other value.
(13/13) And that's it! Our commitment is open and the prover has created all the pieces that the verifier needs to verify the proof!
Stay tuned for part 3, when we use these piece to unequivocally prove that the prover is staying truthful and fulfilling its commitment.
Stay tuned for part 3, when we use these piece to unequivocally prove that the prover is staying truthful and fulfilling its commitment.
Like what you read? Help me spread the word by retweeting the thread (linked below).
Follow me for more explainers and as much alpha as I can possibly serve.
Follow me for more explainers and as much alpha as I can possibly serve.
Loading suggestions...