(1/19)
zkSNARKs are a groundbreaking technology
But they have a newer, shinier cousin:
zkSTARKs
A normie's guide to this fascinating technology🧵
zkSNARKs are a groundbreaking technology
But they have a newer, shinier cousin:
zkSTARKs
A normie's guide to this fascinating technology🧵
(2/19) First, a quick refresher:
zkSNARK is a proof system that allows anyone to prove a statement without ever:
- revealing the underlying information
- interacting with the verifier
Quite a bit of genius
zkSNARK is a proof system that allows anyone to prove a statement without ever:
- revealing the underlying information
- interacting with the verifier
Quite a bit of genius
(3/19) But, zkSNARKs have a few challenges:
1. Trusted Party
To create SNARKs, we rely on a "trusted party" to generate parameters that are used to produce the proof
If anyone gets access to these parameters, they can forge fake proofs
This creates a "backdoor" in the system
1. Trusted Party
To create SNARKs, we rely on a "trusted party" to generate parameters that are used to produce the proof
If anyone gets access to these parameters, they can forge fake proofs
This creates a "backdoor" in the system
(4/19) Why is that bad?
Imagine if a presidential vote took place on a blockchain that was using zkSNARKs to prove the vote count
The trusted party holding the setup parameters could change the proof to tilt the election in their intended direction
Imagine if a presidential vote took place on a blockchain that was using zkSNARKs to prove the vote count
The trusted party holding the setup parameters could change the proof to tilt the election in their intended direction
(5/19)
2. Scalability
As the underlying statement gets more complex, the time to generate & verify proofs increases rapidly in SNARKs
For widespread adoption, we need systems that would allow us to generate & verify the most complex proofs using a simple mobile phone
2. Scalability
As the underlying statement gets more complex, the time to generate & verify proofs increases rapidly in SNARKs
For widespread adoption, we need systems that would allow us to generate & verify the most complex proofs using a simple mobile phone
(6/19)
3. Vulnerability to Quantum Computers
zkSNARKs use cryptographic assumptions which could be broken down if the attacker has a quantum computer
In other words, as computing becomes more advanced, zkSNARKs become more vulnerable to attacks!
3. Vulnerability to Quantum Computers
zkSNARKs use cryptographic assumptions which could be broken down if the attacker has a quantum computer
In other words, as computing becomes more advanced, zkSNARKs become more vulnerable to attacks!
(7/19) Thankfully, in 2018, @EliBenSasson, Iddo Bentov, Yinon Horesh, and @RiabzevMichael came up with a genius solution:
'zkSTARK'
'zero knowledge - Scalable Transparent Argument of Knowledge'
This is in contrast to SNARKs, where 'SN' stands for 'Succinct Non-interactive'
'zkSTARK'
'zero knowledge - Scalable Transparent Argument of Knowledge'
This is in contrast to SNARKs, where 'SN' stands for 'Succinct Non-interactive'
(8/19) zkSTARKs resolve all the above-mentioned weaknesses of zkSNARKs
1. They don't rely on a "trusted setup"
2. They come with much simpler cryptographic assumptions which make them secure even against attackers with quantum computers
3. They are extremely scalable
1. They don't rely on a "trusted setup"
2. They come with much simpler cryptographic assumptions which make them secure even against attackers with quantum computers
3. They are extremely scalable
(9/19) What's the catch?
The size of the proof goes up from 288 bytes to a few hundred kilobytes
This cost isn't worth it at all times, but in public blockchains where the need for trust minimization is high, it makes sense to have a scalable solution like zkSTARK
The size of the proof goes up from 288 bytes to a few hundred kilobytes
This cost isn't worth it at all times, but in public blockchains where the need for trust minimization is high, it makes sense to have a scalable solution like zkSTARK
(10/19) And if elliptic curves break or quantum computers do come around, the higher proof size will definitely be worth it!
zkSTARKs provide something truly unique:
Verifiable trust in a system where there could be very high incentives to try and falsify information
zkSTARKs provide something truly unique:
Verifiable trust in a system where there could be very high incentives to try and falsify information
(11/19) But how do zkSTARKs work?
The process of generating a zkSTARK is quite simple!
Instead of relying on a trusted setup to generate parameters, STARKs use Merkle trees
The process of generating a zkSTARK is quite simple!
Instead of relying on a trusted setup to generate parameters, STARKs use Merkle trees
(12/19) The prover converts the underlying statement into a Merkle Tree and then uses the root of this tree as a source of randomness
This works because:
- Each statement generates a unique Merkle root
- Given just the root, it's impossible to find out the underlying statement
This works because:
- Each statement generates a unique Merkle root
- Given just the root, it's impossible to find out the underlying statement
(13/19) Let's look at an (aggressively) simplified example to understand this:
Say the statement is
"Binance buys out FTX"
The prover converts this into a Merkle Tree like this:
Say the statement is
"Binance buys out FTX"
The prover converts this into a Merkle Tree like this:
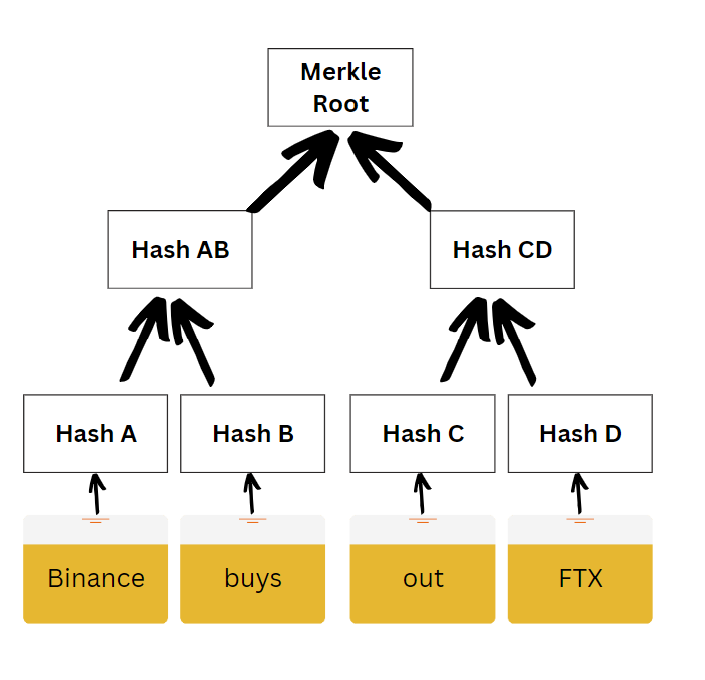
(14/19) The prover then uses this Merkle root in a random number generator
This generator is public and known to everyone
Say this gives out a random number 2
The prover will use this to unveil the 2nd branch in the tree:
"Hash B -> Hash AB -> Merkle Root"
This generator is public and known to everyone
Say this gives out a random number 2
The prover will use this to unveil the 2nd branch in the tree:
"Hash B -> Hash AB -> Merkle Root"
(15/19) Finally, the prover publishes the proof (𝛑)
𝛑 is nothing but a combination of the Merkle root, the unveiled 2nd branch, and the word "buys"
Now anyone can validate 𝛑 easily by verifying that:
𝛑 is nothing but a combination of the Merkle root, the unveiled 2nd branch, and the word "buys"
Now anyone can validate 𝛑 easily by verifying that:
(16/19)
- Hashing "buys" actually returns:
Hash B -> Hash AB -> Merkle root
(Prover is not dishonest)
- The Merkle root generates the random number 2
(Prover is "committed" to the original statement)
- Hashing "buys" actually returns:
Hash B -> Hash AB -> Merkle root
(Prover is not dishonest)
- The Merkle root generates the random number 2
(Prover is "committed" to the original statement)
(17/19) In this simple manner, zkSTARKs form a robust proof system while revealing nothing about the statement
'Don't they reveal the word "buys"?'
In this simplified example, yes. In reality, the statement is hidden beneath a secret polynomial
'Don't they reveal the word "buys"?'
In this simplified example, yes. In reality, the statement is hidden beneath a secret polynomial
(18/19) The Merkle trees are also HUGE and the prover often publishes several branches (and not just 1)
This ensures that the probability of a malicious prover cheating the system is negligible
@StarkWareLtd has been actively using STARKs for protocols like @StarkNetEco
This ensures that the probability of a malicious prover cheating the system is negligible
@StarkWareLtd has been actively using STARKs for protocols like @StarkNetEco
(19/19) Further research is underway to make the proof size in STARKs smaller
If you want to dive into the math behind STARKs, I would recommend beginning with @VitalikButerin's blogs on the topic
@EliBenSasson also published a mega-thread with some awesome resources
If you want to dive into the math behind STARKs, I would recommend beginning with @VitalikButerin's blogs on the topic
@EliBenSasson also published a mega-thread with some awesome resources
I hope you learned something new!
Follow me @ShivanshuMadan for more such content
Like/Retweet the first tweet below to help me spread the word
Follow me @ShivanshuMadan for more such content
Like/Retweet the first tweet below to help me spread the word
Loading suggestions...