This will surprise you: sine and cosine are orthogonal to each other.
What does orthogonality even mean for functions? In this thread, we'll use the superpower of abstraction to go far beyond our intuition.
We'll also revolutionize science on the way.
What does orthogonality even mean for functions? In this thread, we'll use the superpower of abstraction to go far beyond our intuition.
We'll also revolutionize science on the way.
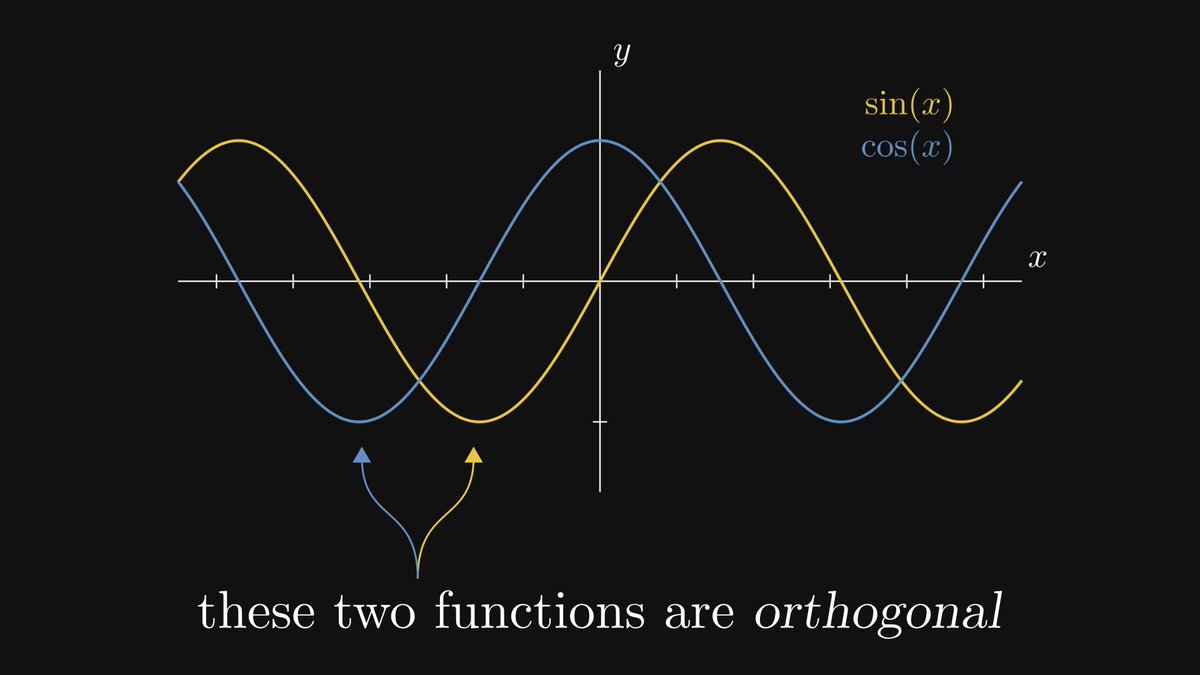
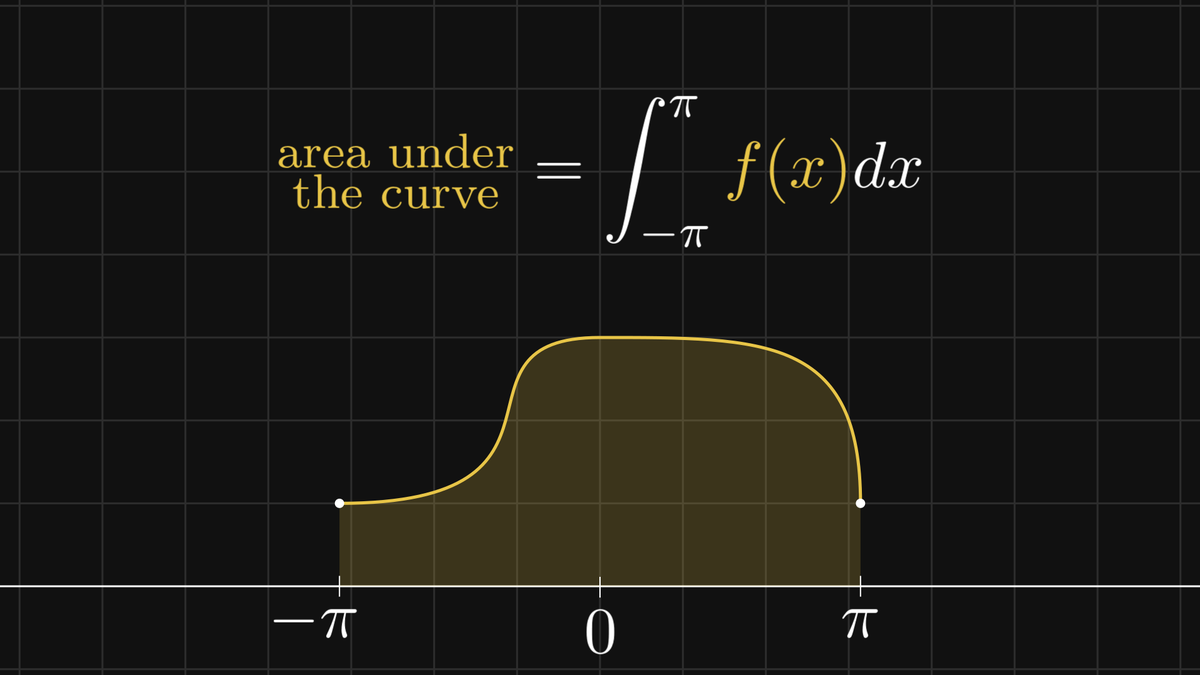
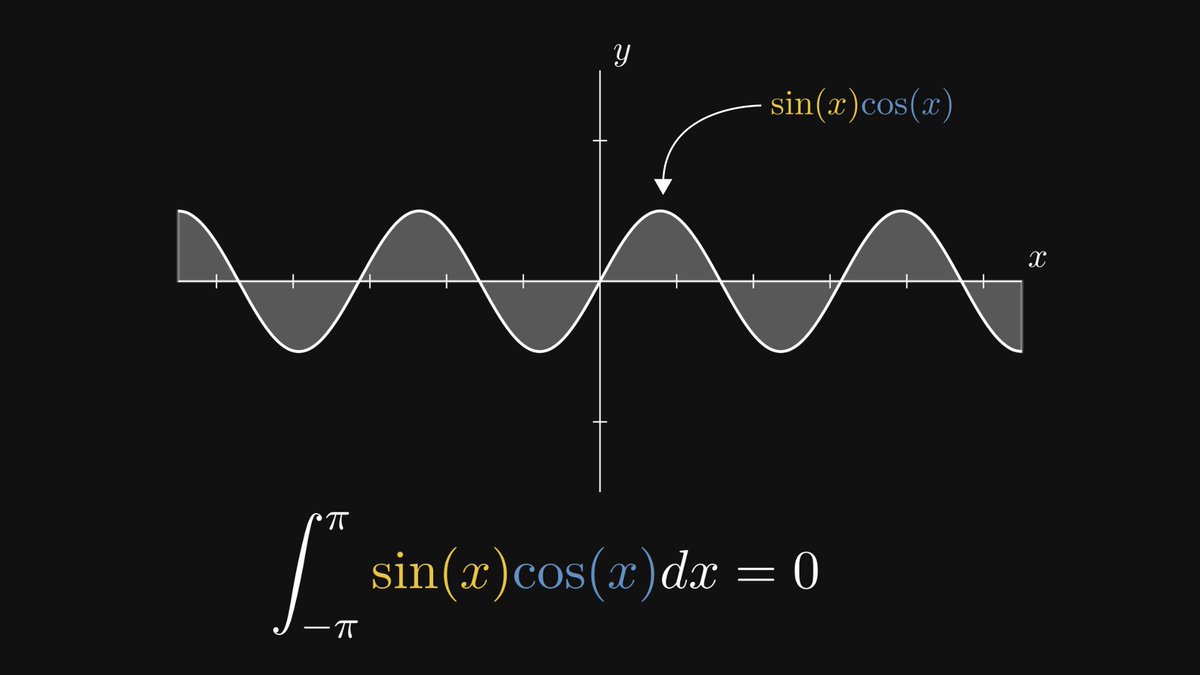
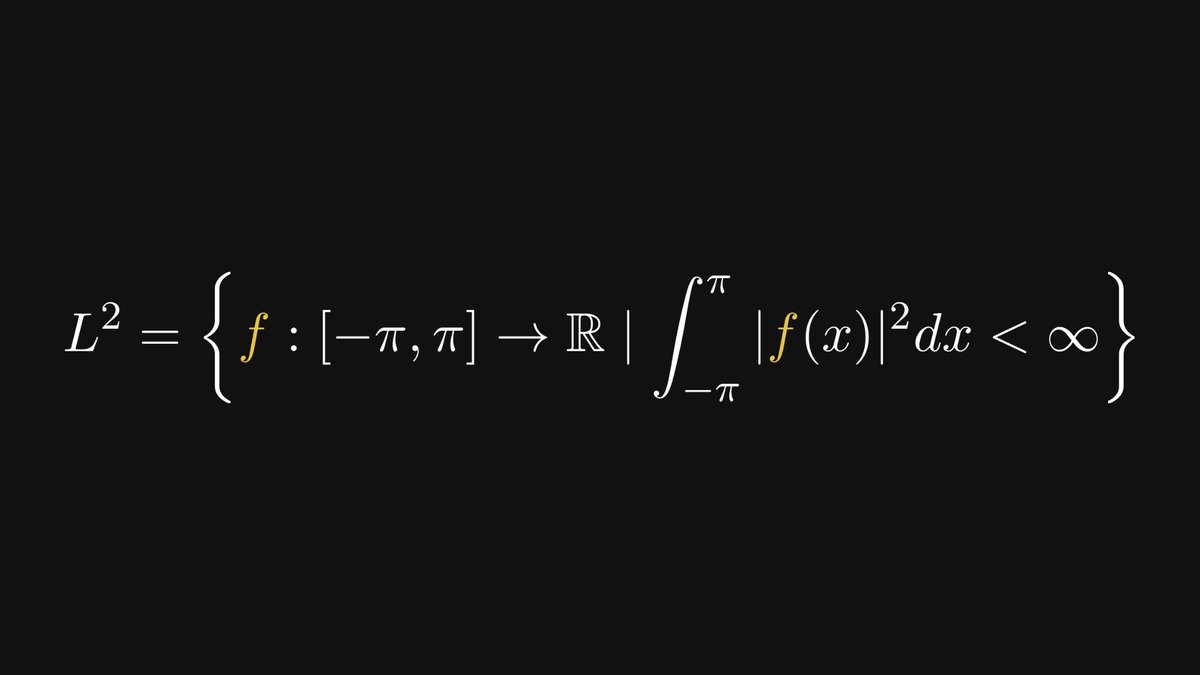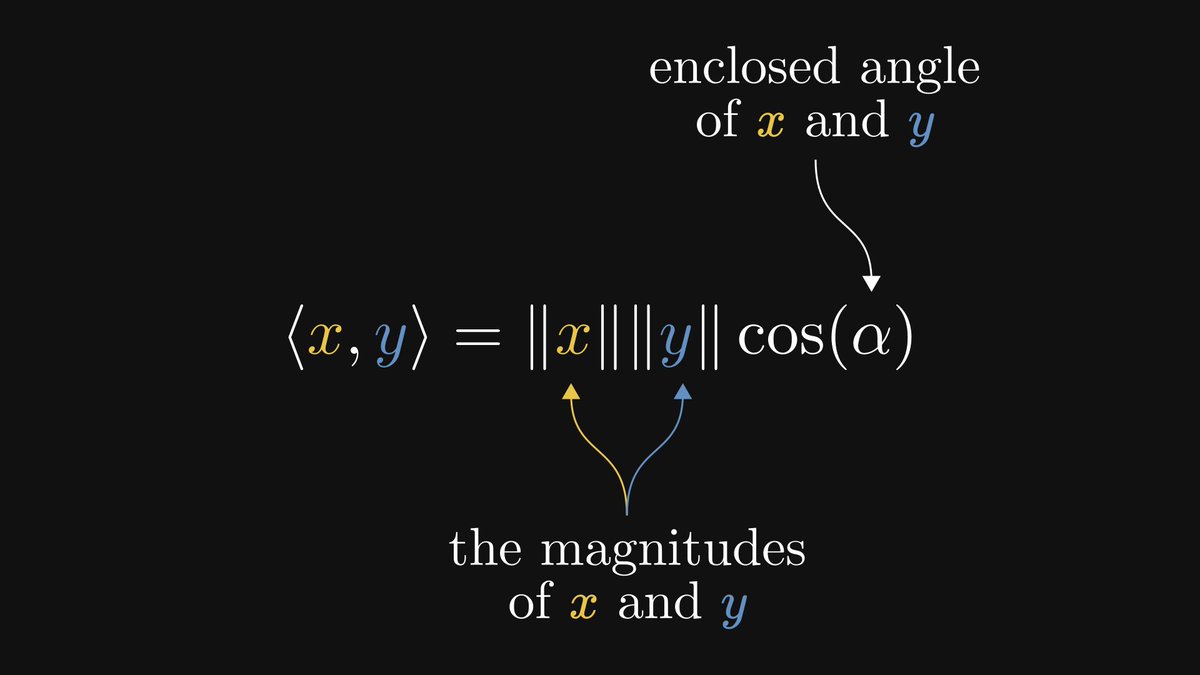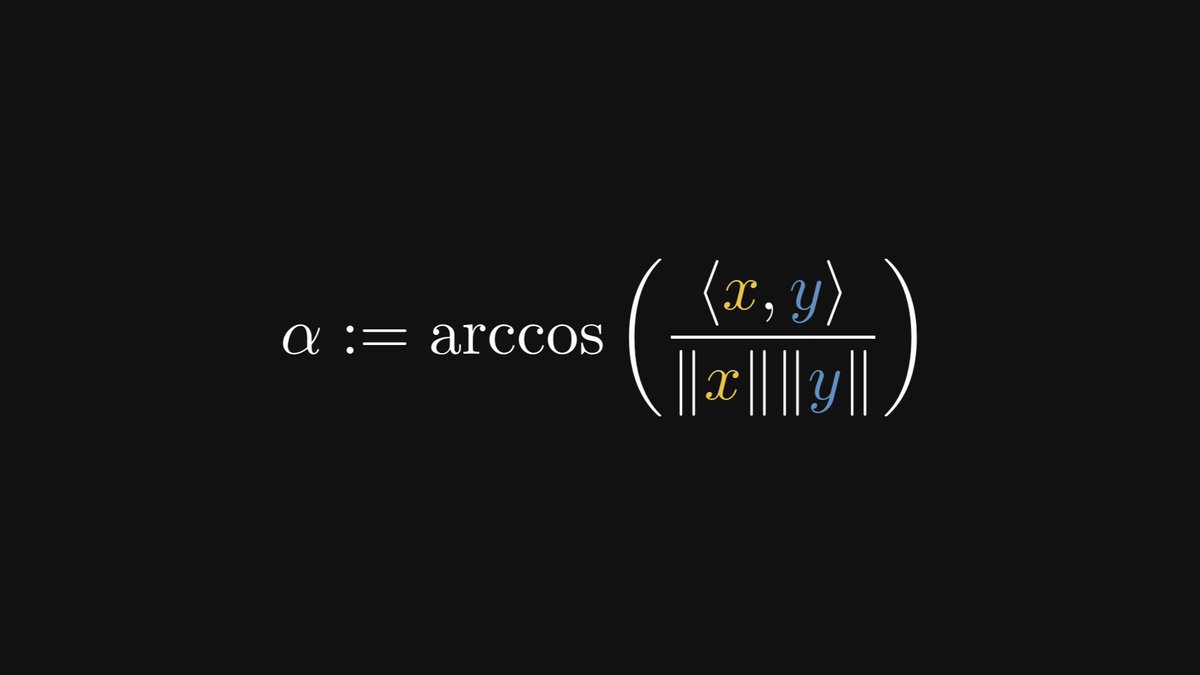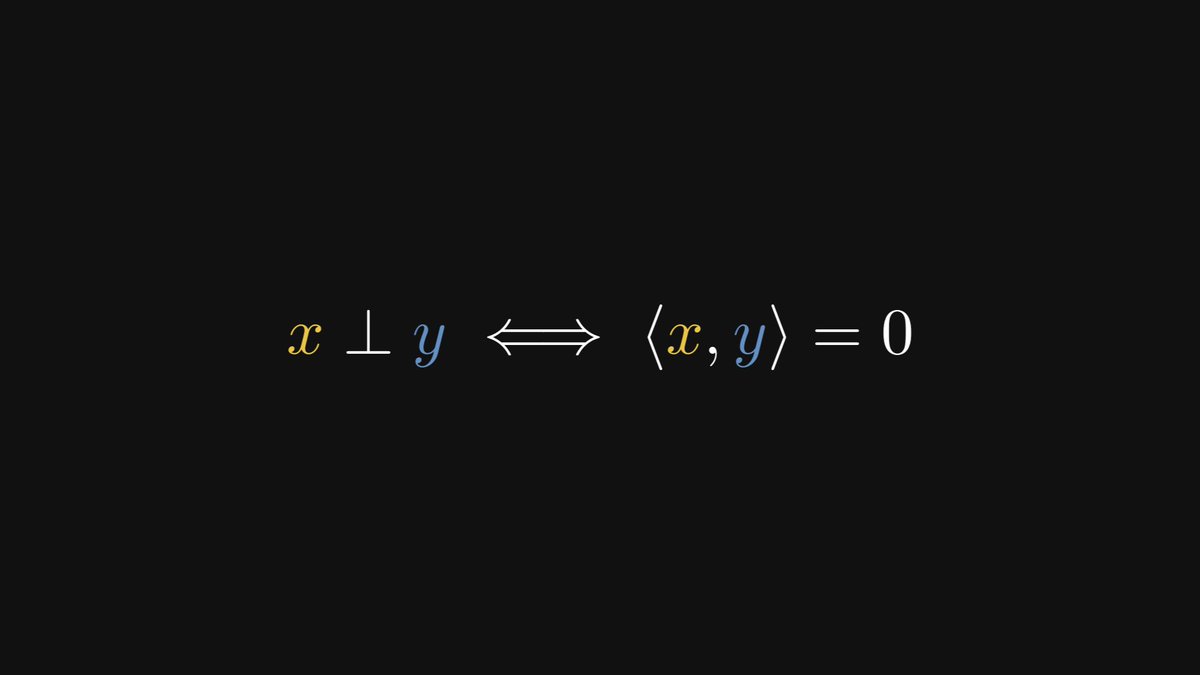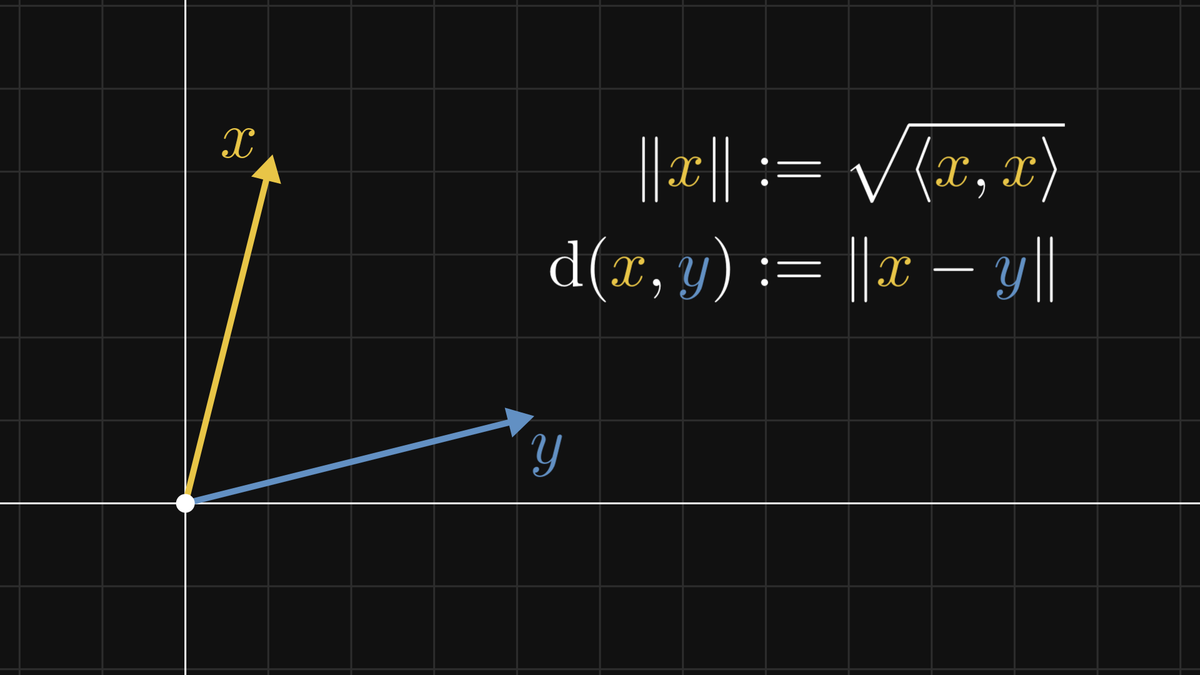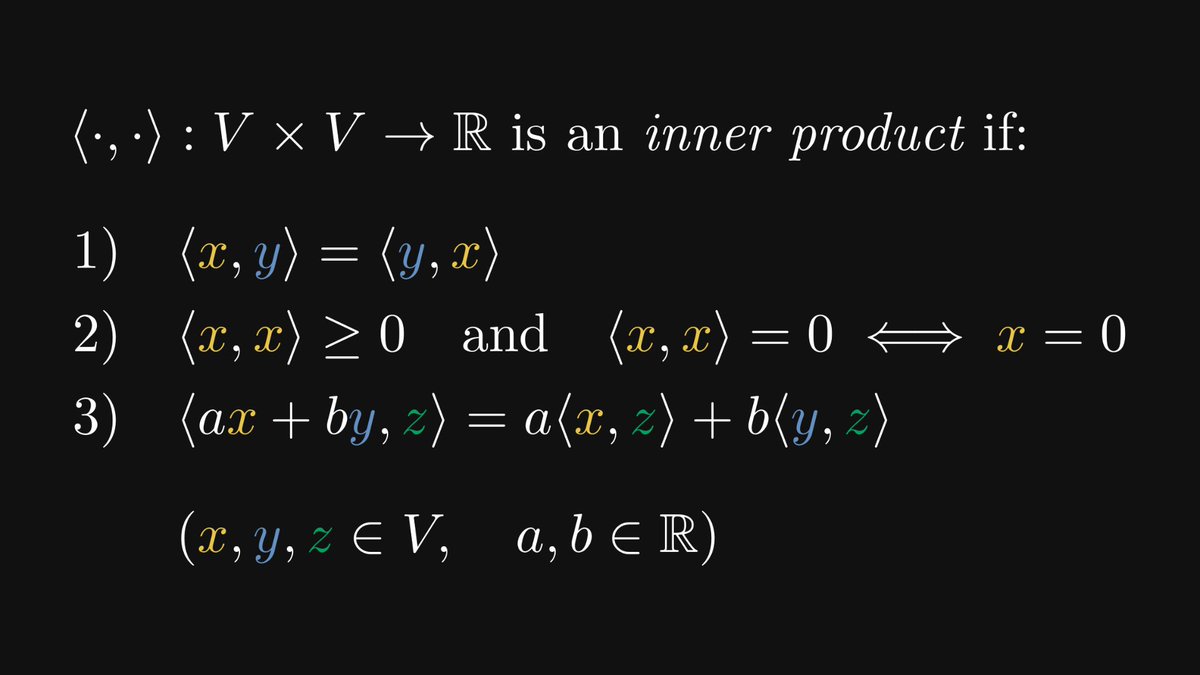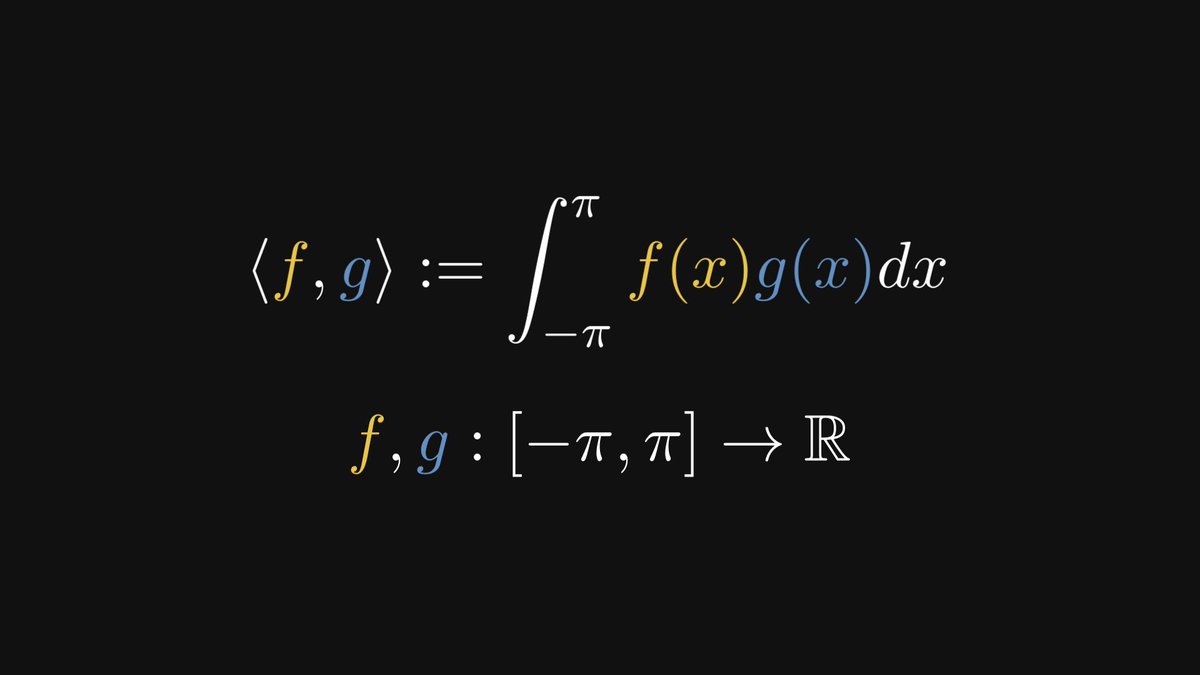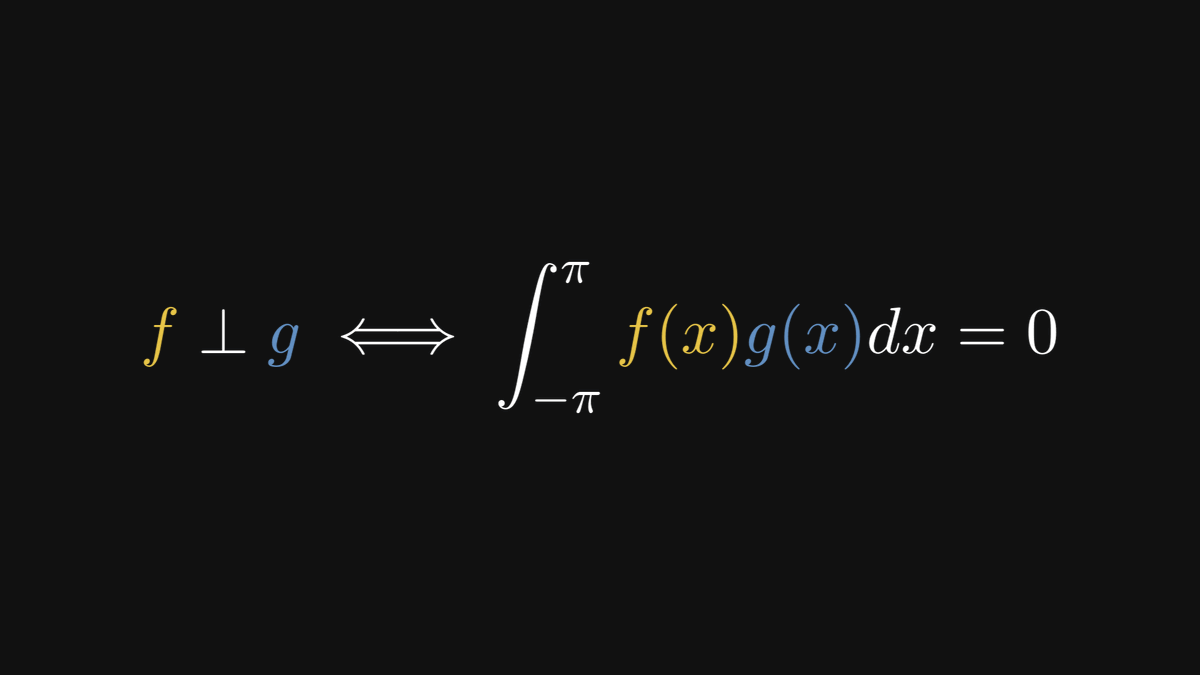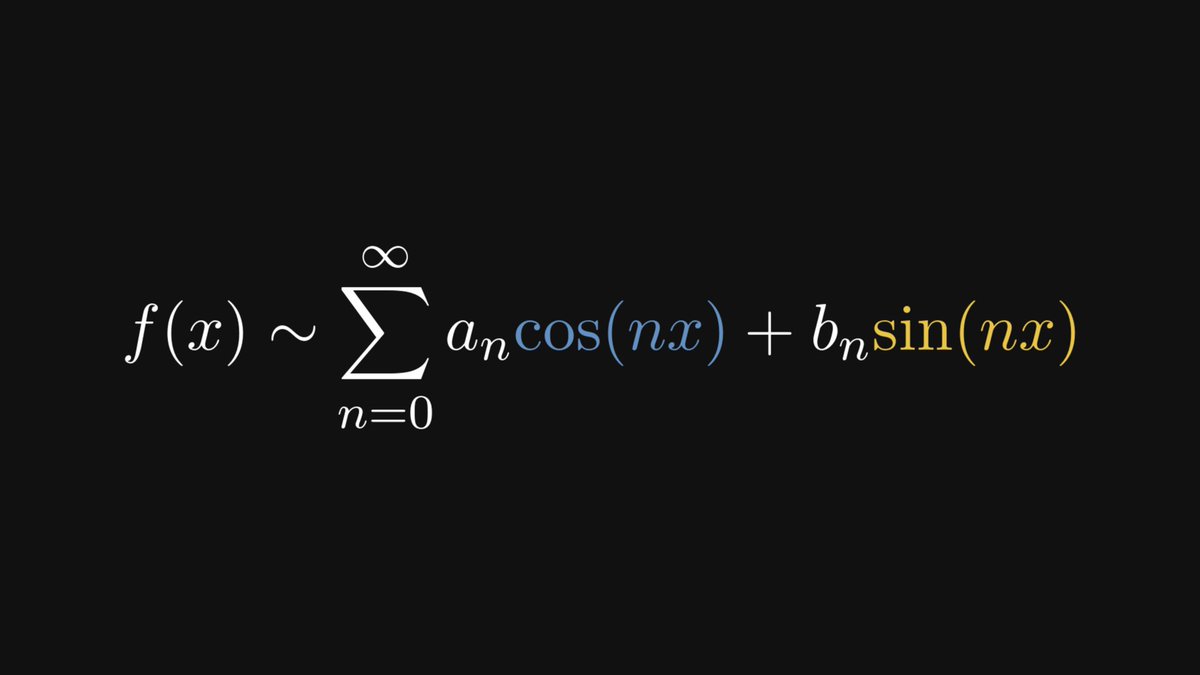Our journey ahead has three milestones. We'll
1. generalize the concept of a vector,
2. show what angles really are,
3. and see what functions have to do with all this.
Here we go!
1. generalize the concept of a vector,
2. show what angles really are,
3. and see what functions have to do with all this.
Here we go!
Let's start with vectors. On the plane, vectors are simply arrows.
The concept of angle is intuitive as well. According to Wikipedia, an angle “is the figure formed by two rays”.
How can we define this for functions?
The concept of angle is intuitive as well. According to Wikipedia, an angle “is the figure formed by two rays”.
How can we define this for functions?
What makes a vector? Two things: vector addition and scalar multiplication. We can take the core properties of these operations and turn them into a definition!
This is the process of abstraction.
This is the process of abstraction.
Thus, any set V with addition and scalar multiplication fulfilling the properties below is a vector space.
The elements of a vector space are called vectors.
The elements of a vector space are called vectors.
Following this, we can form vector spaces from functions!
One prime example is the so-called L²-space, consisting of functions whose square-integral is finite.
This is a technical condition, but the gist is: sine and cosine belong here.
One prime example is the so-called L²-space, consisting of functions whose square-integral is finite.
This is a technical condition, but the gist is: sine and cosine belong here.
Moving on to angles. Can we find a generalizable definition?
The Wikipedia version "the figure formed by two rays" won't cut it.
The Wikipedia version "the figure formed by two rays" won't cut it.
On the Euclidean plane, we can turn to the inner product! (Also known as the dot product.)
There, the enclosed angle appears explicitly.
There, the enclosed angle appears explicitly.
We can express the angle from this expression and even use it to define it!
Why is this good for us? Because it's an algebraic definition, not reliant on intuitive concepts such as "the figure formed by two rays".
Why is this good for us? Because it's an algebraic definition, not reliant on intuitive concepts such as "the figure formed by two rays".
The general definition of orthogonality also follow.
We call two vectors orthogonal if their inner product is zero. You can verify this using the definition above.
We call two vectors orthogonal if their inner product is zero. You can verify this using the definition above.
To define the concept of angle in a general vector space, we only need one thing: an inner product.
(Distance and magnitude stems for the inner product whenever the latter one is available.)
(Distance and magnitude stems for the inner product whenever the latter one is available.)
So, what is an inner product?
We'll do what we've done before two times: identify the core properties of the Euclidean inner product that we know, then turn it into a definition.
In this case, we have three such properties.
We'll do what we've done before two times: identify the core properties of the Euclidean inner product that we know, then turn it into a definition.
In this case, we have three such properties.
Now we are almost there!
Is there an inner product for the L²-space?
Yes, and it is given by the Riemann integral!
Is there an inner product for the L²-space?
Yes, and it is given by the Riemann integral!
If you are not familiar with the Riemann integral, I got you.
In essence, the Riemann integral of a function over a given interval is just the signed area between the function's graph and the x-axis.
It's signed because if the graph goes below the x-axis, the area is negative.
In essence, the Riemann integral of a function over a given interval is just the signed area between the function's graph and the x-axis.
It's signed because if the graph goes below the x-axis, the area is negative.
Now, what is the analogue of orthogonality in the L²-space?
Two functions are orthogonal if the integral of their product is zero. It's not intuitive, but this is the power of abstraction: we have the power to move way beyond our limited intuition!
Two functions are orthogonal if the integral of their product is zero. It's not intuitive, but this is the power of abstraction: we have the power to move way beyond our limited intuition!
Back to the case of sine and cosine. Why are they orthogonal?
Because their product is an odd function. Thus, the signed area between the graph and the x-axis is zero.
Because their product is an odd function. Thus, the signed area between the graph and the x-axis is zero.
This feels like a mathematical curio, but trust me, it is not.
Recall the "revolutionizing science" part I mentioned at the start? This is it.
The orthogonality of trigonometric functions is the cornerstone of modern technology. We wouldn't even have JPEG-s without them.
Recall the "revolutionizing science" part I mentioned at the start? This is it.
The orthogonality of trigonometric functions is the cornerstone of modern technology. We wouldn't even have JPEG-s without them.
This thread is part of the latest issue of The Palindrome.
In the full post, I go into the details of
- the process of abstraction,
- why is the L² inner product a natural idea,
and much more!
thepalindrome.substack.com
In the full post, I go into the details of
- the process of abstraction,
- why is the L² inner product a natural idea,
and much more!
thepalindrome.substack.com
If you have enjoyed this thread, share it with your friends and follow me!
I regularly post deep-dive explanations about big ideas and complex concepts.
Understanding mathematics will make you a smarter person, and I want to help you with that.
I regularly post deep-dive explanations about big ideas and complex concepts.
Understanding mathematics will make you a smarter person, and I want to help you with that.
Loading suggestions...