1/N
This is a thread on how ancient Hindu & Jain Indian mathematicians approached the study of mensurations of quadrilaterals & cyclic quadrilaterals.
This is a thread on how ancient Hindu & Jain Indian mathematicians approached the study of mensurations of quadrilaterals & cyclic quadrilaterals.
2/N
Specifically we are going to trace the events surrounding quadrilateral, cyclic quadrilateral & its diagonals analyzed by Indian mathematicians as recorded in texts such as ÅulbasÅ«tras, BrÄhmasphuį¹asiddhÄnta, Gaį¹itasÄrasaį¹ graha, LÄ«lÄvatÄ« etc.
Specifically we are going to trace the events surrounding quadrilateral, cyclic quadrilateral & its diagonals analyzed by Indian mathematicians as recorded in texts such as ÅulbasÅ«tras, BrÄhmasphuį¹asiddhÄnta, Gaį¹itasÄrasaį¹ graha, LÄ«lÄvatÄ« etc.
3/N
A cyclic quadrilateral is a quadrilateral that can be inscribed in a circle. Four points A, B, C, and D are called concylic if they all lie on the same circle
A cyclic quadrilateral is a quadrilateral that can be inscribed in a circle. Four points A, B, C, and D are called concylic if they all lie on the same circle
4/N
An examination of the earliest known geometry in India, Vedic geometry, involves a study of the ÅulbasÅ«tras, conservatively dated as recorded no later than 800 BCE, though they certainly contain knowledge from earlier times.
An examination of the earliest known geometry in India, Vedic geometry, involves a study of the ÅulbasÅ«tras, conservatively dated as recorded no later than 800 BCE, though they certainly contain knowledge from earlier times.
5/N
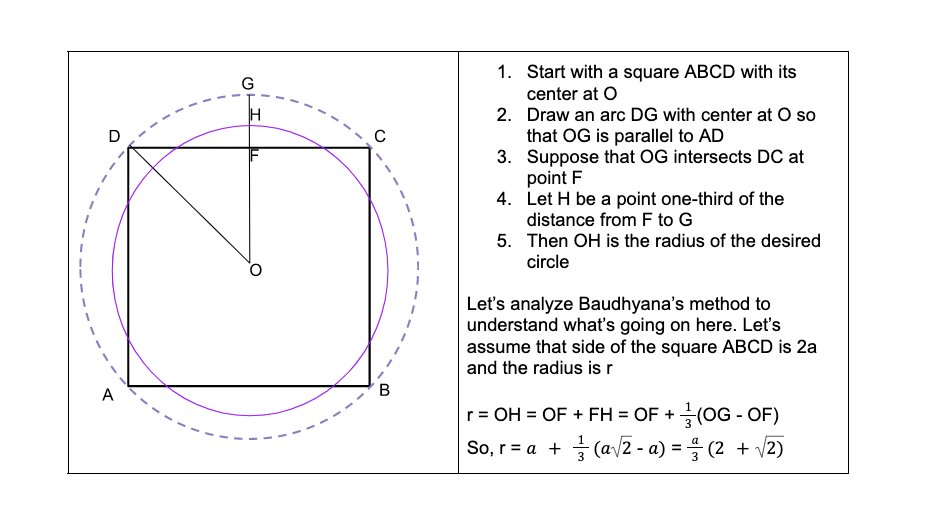
The first indirect reference to a cyclic square is mentioned in Baudhayana ÅulbasÅ«tra 1.58 in the context of transforming a square or finding a circle area is approximately close to that of a given square
The first indirect reference to a cyclic square is mentioned in Baudhayana ÅulbasÅ«tra 1.58 in the context of transforming a square or finding a circle area is approximately close to that of a given square
6/N
The same method is also provided by Apasthambha (3. 2) and Katyayana ÅulbasÅ«tra (3.13). The sutras are attached in the image
The same method is also provided by Apasthambha (3. 2) and Katyayana ÅulbasÅ«tra (3.13). The sutras are attached in the image
7/N
Baudhayana ÅulbasÅ«tra 1.58 prescribes a recipe on how to geometrically transform a square to a circle with approximate equal area. In the process, an intermediate reference to a cyclic square comes up. The details are given with modern notation below
Baudhayana ÅulbasÅ«tra 1.58 prescribes a recipe on how to geometrically transform a square to a circle with approximate equal area. In the process, an intermediate reference to a cyclic square comes up. The details are given with modern notation below
8/N
Brahmagupta, a genius Indian Hindu astronomer & mathematician authored two treatises in Sanskrit, BrÄhmasphuį¹asiddhÄnta & Khaį¹įøakhdyaka no later than 620 AD. BrÄhmasphuį¹asiddhÄnta was translated into Arabic about 770 AD & had a major impact on Islamic mathematics.
Brahmagupta, a genius Indian Hindu astronomer & mathematician authored two treatises in Sanskrit, BrÄhmasphuį¹asiddhÄnta & Khaį¹įøakhdyaka no later than 620 AD. BrÄhmasphuį¹asiddhÄnta was translated into Arabic about 770 AD & had a major impact on Islamic mathematics.
9/N
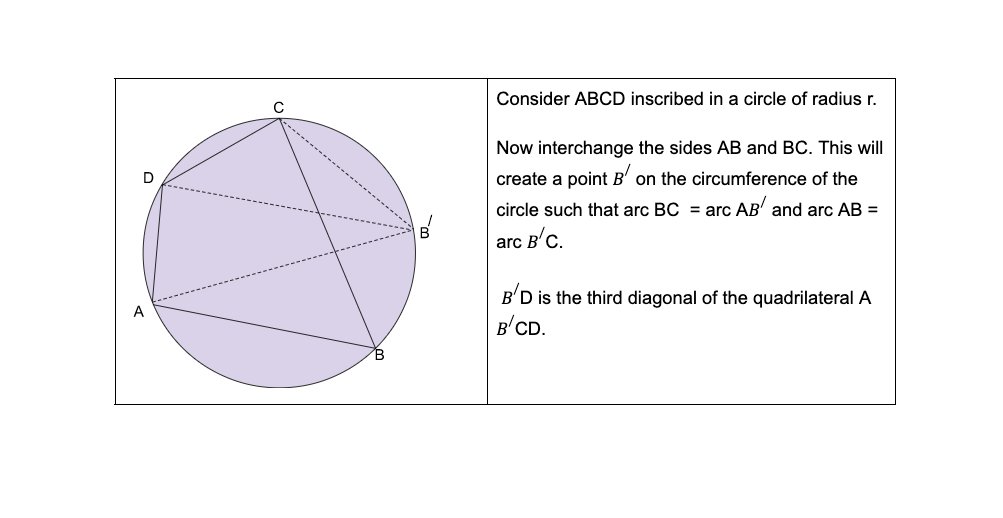
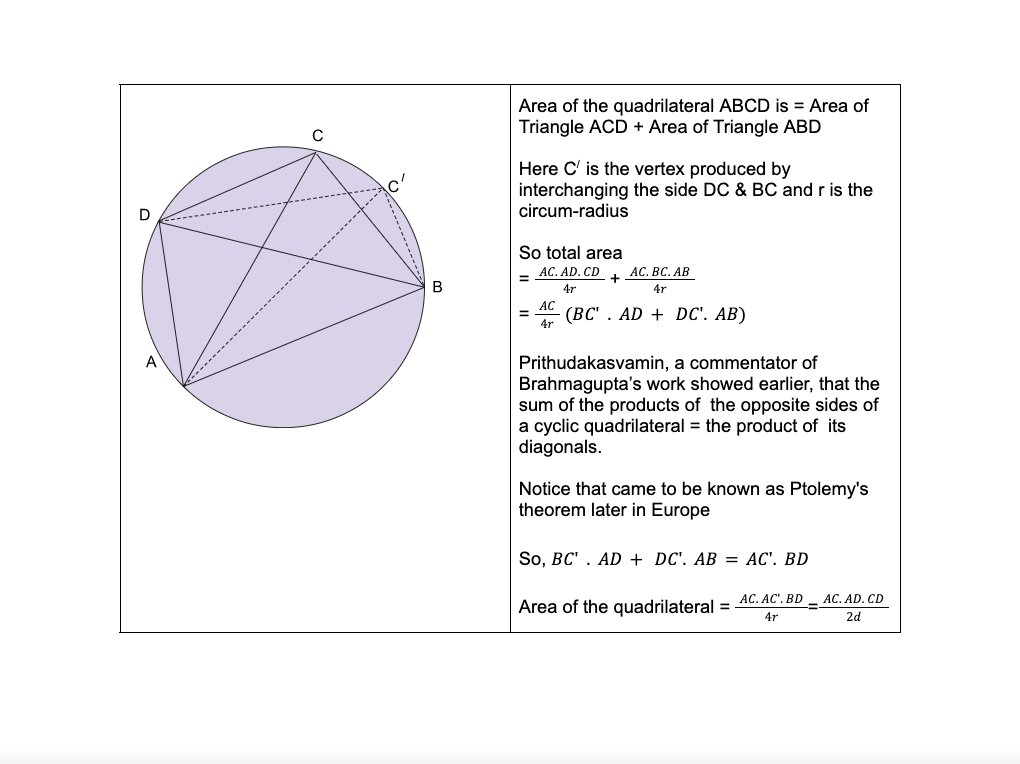
In BrÄhmasphuį¹asiddhÄnta 12.21, Brahmagupta provides a formula for area of a cyclic quadrilateral
In BrÄhmasphuį¹asiddhÄnta 12.21, Brahmagupta provides a formula for area of a cyclic quadrilateral
10/N
BrÄhmasphuį¹asiddhÄnta, 12.21
The gross area of a cyclic quadrilateral is the product of half the sums of the opposite sides; the exact area is the square root of the product of four sets of half the sum of the sides respectively diminished by sides.
BrÄhmasphuį¹asiddhÄnta, 12.21
The gross area of a cyclic quadrilateral is the product of half the sums of the opposite sides; the exact area is the square root of the product of four sets of half the sum of the sides respectively diminished by sides.
11/N
BrÄhmasphuį¹asiddhÄnta Sutra 12.21 says the area A of a cyclic quadrilateral with sides a, b, c and d, whereas S is half of the perimeter of the cyclic quadrilateral is given as shown below
A =Square Root of [ (S-a)(S-b)(S-c)(S-d) ]
BrÄhmasphuį¹asiddhÄnta Sutra 12.21 says the area A of a cyclic quadrilateral with sides a, b, c and d, whereas S is half of the perimeter of the cyclic quadrilateral is given as shown below
A =Square Root of [ (S-a)(S-b)(S-c)(S-d) ]
12/N
Some modern scholars have erroneously interpreted ą¤¤ą„ą¤°ą¤æą¤ą¤¤ą„ą¤°ą„ą¤ą„ą¤ (trichaturbhuja) in the above sutra as referring to the sutra being applicable to triangles and quadrilaterals (independently).
Some modern scholars have erroneously interpreted ą¤¤ą„ą¤°ą¤æą¤ą¤¤ą„ą¤°ą„ą¤ą„ą¤ (trichaturbhuja) in the above sutra as referring to the sutra being applicable to triangles and quadrilaterals (independently).
13/N
The term ą¤¤ą„ą¤°ą¤æą¤ą¤¤ą„ą¤°ą„ą¤ą„ą¤ was used by Brahmagupta to refer to a cyclic quadrilateral (and not triangle and/or quadrilateral by itself).
The term ą¤¤ą„ą¤°ą¤æą¤ą¤¤ą„ą¤°ą„ą¤ą„ą¤ was used by Brahmagupta to refer to a cyclic quadrilateral (and not triangle and/or quadrilateral by itself).
14/N
Other than Sutra 12.21, the only other place where the term ą¤¤ą„ą¤°ą¤æą¤ą¤¤ą„ą¤°ą„ą¤ą„ą¤ occurs in BrÄhmasphuį¹asiddhÄnta, is in sutra 12.27. There the result involved is stated first for a triangle, separately, and then for a ą¤¤ą„ą¤°ą¤æą¤ą¤¤ą„ą¤°ą„ą¤ą„ą¤.
Other than Sutra 12.21, the only other place where the term ą¤¤ą„ą¤°ą¤æą¤ą¤¤ą„ą¤°ą„ą¤ą„ą¤ occurs in BrÄhmasphuį¹asiddhÄnta, is in sutra 12.27. There the result involved is stated first for a triangle, separately, and then for a ą¤¤ą„ą¤°ą¤æą¤ą¤¤ą„ą¤°ą„ą¤ą„ą¤.
15/N
This clearly indicates that the term ą¤¤ą„ą¤°ą¤æą¤ą¤¤ą„ą¤°ą„ą¤ą„ą¤ is used independently to refer to a cyclic quadrilateral by Brahmagupta in BrÄhmasphuį¹asiddhÄnta
This clearly indicates that the term ą¤¤ą„ą¤°ą¤æą¤ą¤¤ą„ą¤°ą„ą¤ą„ą¤ is used independently to refer to a cyclic quadrilateral by Brahmagupta in BrÄhmasphuį¹asiddhÄnta
16/N
Brahmagupta while pursuing his study of triangles dealt with the circumcircle, described in particular a formula for the circum-radius, and considered quadrilaterals formed by the triangle and a point on the circumcircle, which motivated the term ą¤¤ą„ą¤°ą¤æą¤ą¤¤ą„ą¤°ą„ą¤ą„ą¤.
Brahmagupta while pursuing his study of triangles dealt with the circumcircle, described in particular a formula for the circum-radius, and considered quadrilaterals formed by the triangle and a point on the circumcircle, which motivated the term ą¤¤ą„ą¤°ą¤æą¤ą¤¤ą„ą¤°ą„ą¤ą„ą¤.
17/N
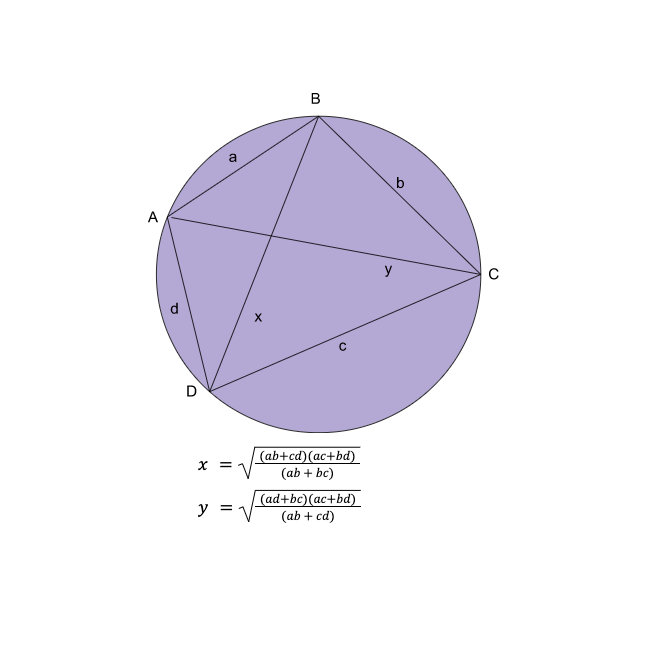
Brahmagupta also provides the mechanism to find out the diagonals of a cyclic quadrilateral in BrÄhmasphuį¹asiddhÄnta 12.28
Brahmagupta also provides the mechanism to find out the diagonals of a cyclic quadrilateral in BrÄhmasphuį¹asiddhÄnta 12.28
18/N
BrÄhmasphuį¹asiddhÄnta 12.28
The sums of the products of the sides about both the diagonals should be divided by each other and multiplied by the sum of the products of the opposite sides. The square roots of the quotients are the diagonals in visama quadrilateral.
BrÄhmasphuį¹asiddhÄnta 12.28
The sums of the products of the sides about both the diagonals should be divided by each other and multiplied by the sum of the products of the opposite sides. The square roots of the quotients are the diagonals in visama quadrilateral.
19/N
In contemporary notations, we can describe BrÄhmasphuį¹asiddhÄnta: 12.28 as shown below
In contemporary notations, we can describe BrÄhmasphuį¹asiddhÄnta: 12.28 as shown below
20/N
A 3rd significant contribution by Brahmagupta for cyclic quadrilateral is a method on how to get a rational cyclic quadrilateral, which is to multiply the sides of two rational right triangles by each other's hypotenuse & use them as the sides of the quadrilateral.
A 3rd significant contribution by Brahmagupta for cyclic quadrilateral is a method on how to get a rational cyclic quadrilateral, which is to multiply the sides of two rational right triangles by each other's hypotenuse & use them as the sides of the quadrilateral.
21/N
BrÄhmasphuį¹asiddhÄnta 12:26
The circum-radius of a visama quadrilateral is half the square root of the sum of the squares of opposite sides
BrÄhmasphuį¹asiddhÄnta 12:26
The circum-radius of a visama quadrilateral is half the square root of the sum of the squares of opposite sides
22/N
Brahmgupta gives specific direction for forming the rational quadrilateral in BrÄhmasphuį¹asiddhÄnta 12.38
Brahmgupta gives specific direction for forming the rational quadrilateral in BrÄhmasphuį¹asiddhÄnta 12.38
23/N
āThe kotis and bhujas of two jatyas multiplied by each other's hypotenuse are the four sides in a visama quadrilateral. The longest is the base, the least the face and the remaining two sides the flanksā
āThe kotis and bhujas of two jatyas multiplied by each other's hypotenuse are the four sides in a visama quadrilateral. The longest is the base, the least the face and the remaining two sides the flanksā
24/N
In the post-Brahmagupta period, there has been a rich legacy of analysis for geometrical mensurations of cyclic quadrilateral by the Indian mathematicians.
In the post-Brahmagupta period, there has been a rich legacy of analysis for geometrical mensurations of cyclic quadrilateral by the Indian mathematicians.
25/N
The brilliant Indian Jaina mathematician MahÄvÄ«ra (no later than 800 CE) also provides area of a cyclic quadrilateral in Gaį¹itasÄrasaį¹ graha 7.50 much along the line of what is mentioned in BrÄhmasphuį¹asiddhÄnta (continued..)
The brilliant Indian Jaina mathematician MahÄvÄ«ra (no later than 800 CE) also provides area of a cyclic quadrilateral in Gaį¹itasÄrasaį¹ graha 7.50 much along the line of what is mentioned in BrÄhmasphuį¹asiddhÄnta (continued..)
26/N
Gaį¹itasÄrasaį¹ graha 7.50
Four quantities represented (respectively) by half the sum of the sides as diminished by (each of) the sides (taken in order) are multiplied together and the square root (of the product so obtained) gives the minutely accurate measure
Gaį¹itasÄrasaį¹ graha 7.50
Four quantities represented (respectively) by half the sum of the sides as diminished by (each of) the sides (taken in order) are multiplied together and the square root (of the product so obtained) gives the minutely accurate measure
27/N
The second half of the above mentioned verse is the usual formula for the area of a trapezium, as the product of the perpendicular height with half the sum of the base and the opposite side, mentioning also a caveat that it does not hold for a viį¹£amacaturasra
The second half of the above mentioned verse is the usual formula for the area of a trapezium, as the product of the perpendicular height with half the sum of the base and the opposite side, mentioning also a caveat that it does not hold for a viį¹£amacaturasra
28/N
In his seminal book PÄtÄ«gaį¹ita, the Hindu mathematician ÅrÄ«dhara (no later than 870 CE) also gives a formula for area of a quadrilateral which is very similar to what was mentioned in Brahmaguptaās BrÄhmasphuį¹asiddhÄnta
In his seminal book PÄtÄ«gaį¹ita, the Hindu mathematician ÅrÄ«dhara (no later than 870 CE) also gives a formula for area of a quadrilateral which is very similar to what was mentioned in Brahmaguptaās BrÄhmasphuį¹asiddhÄnta
29/N
Thus ÅrÄ«dhara seems to have given the formula for the area of any general quadrilateral. He did not specifically mention the applicability for a cyclic quadrilateral.
Thus ÅrÄ«dhara seems to have given the formula for the area of any general quadrilateral. He did not specifically mention the applicability for a cyclic quadrilateral.
30/N
ÅrÄ«dhara makes an assumption that the above formula is for all general quadrilaterals and then proceeds to mildly criticize its accuracy.
ÅrÄ«dhara makes an assumption that the above formula is for all general quadrilaterals and then proceeds to mildly criticize its accuracy.
31/N
ÅrÄ«dhara says - āBut this result is only true for those quadrilaterals where the difference between altitude and flank sides is small. In case these conditions are not met, the result would not be correctā
ÅrÄ«dhara says - āBut this result is only true for those quadrilaterals where the difference between altitude and flank sides is small. In case these conditions are not met, the result would not be correctā
32/N
The genius Hindu mathematician Bhaskaracharya II also provides the same method for computing the area of a quadrilateral (no later than 1114 CE)
The genius Hindu mathematician Bhaskaracharya II also provides the same method for computing the area of a quadrilateral (no later than 1114 CE)
33/N
In his groundbreaking work "Lilavati", Bhaskara mentions in sutra 175: From half the sum of all the (four) sides subtract each side separately and take their product. Square-root of this product is an imprecise area of quadrilateral.
In his groundbreaking work "Lilavati", Bhaskara mentions in sutra 175: From half the sum of all the (four) sides subtract each side separately and take their product. Square-root of this product is an imprecise area of quadrilateral.
34/N
However Bhaskara also perhaps makes an assumption (erroneously) that this method was prescribed by Brahmagupta for a general purpose quadrilateral. He does not seem to specify that the original intent of Brahmaguptaās method was ONLY meant for a cyclic quadrilateral.
However Bhaskara also perhaps makes an assumption (erroneously) that this method was prescribed by Brahmagupta for a general purpose quadrilateral. He does not seem to specify that the original intent of Brahmaguptaās method was ONLY meant for a cyclic quadrilateral.
35/N
Bhaskara then goes on to criticize Brahmaguptaās (correct) method which was meant for cyclic quadrilaterals based on the assumption that the method was meant for all types of quadrilaterals.
Bhaskara then goes on to criticize Brahmaguptaās (correct) method which was meant for cyclic quadrilaterals based on the assumption that the method was meant for all types of quadrilaterals.
36/N
Lilavati 177: Formula for the area of a quadrilateral is not accurate. This is so because the lengths of its diagonals are indeterminate. So how can we get an accurate value? Ancient mathematicians had fixed some values for the diagonals but they are not valid in all cases
Lilavati 177: Formula for the area of a quadrilateral is not accurate. This is so because the lengths of its diagonals are indeterminate. So how can we get an accurate value? Ancient mathematicians had fixed some values for the diagonals but they are not valid in all cases
37/N
However cyclic quadrilaterals make a comeback in Indian mathematics once again in Narayana Panditaās work in the 14th century.
However cyclic quadrilaterals make a comeback in Indian mathematics once again in Narayana Panditaās work in the 14th century.
38/N
Narayana Pandita was born in Uttar Pradesh, India about 1340 and known for three important texts on mathematics: Ganita Kaumudi. Bijganita Vatamsa and Karma Pradipika.
Narayana Pandita was born in Uttar Pradesh, India about 1340 and known for three important texts on mathematics: Ganita Kaumudi. Bijganita Vatamsa and Karma Pradipika.
39/N
Narayana Pandita honors Brahmaguptaās original work by literally citing the same formula for computation of area for cyclic quadrilateral in his work Ganita Kaumudi.
Narayana Pandita honors Brahmaguptaās original work by literally citing the same formula for computation of area for cyclic quadrilateral in his work Ganita Kaumudi.
40/N
Ganita Kaumudi - 46: Divide the sum of the products of the sides about both the diagonals by each other. Multiply the quotients by the sum of the products of opposite sides. Square roots of the products are the diagonals in a quadrilateral.
Ganita Kaumudi - 46: Divide the sum of the products of the sides about both the diagonals by each other. Multiply the quotients by the sum of the products of opposite sides. Square roots of the products are the diagonals in a quadrilateral.
41/N
Ganita Kaumudi 48 can be described using modern notation as below
Ganita Kaumudi 48 can be described using modern notation as below
42/N
Narayana Pandita then provides another method for computing the area of a cyclic quadrilateral then in terms of these three diagonals. When the product of the three diagonals is divided by twice the circum-diameter, we get the area
Narayana Pandita then provides another method for computing the area of a cyclic quadrilateral then in terms of these three diagonals. When the product of the three diagonals is divided by twice the circum-diameter, we get the area
43/N
Ganita Kaumudi 52 is described using modern notation in the attached image below
Ganita Kaumudi 52 is described using modern notation in the attached image below
44/N
A proof of Brahmaguptaās method for finding area of cyclic quadrilateral is given by the Indian Hindu mathematician Jyeį¹£į¹hadeva (c.ā1500 ā c.ā1575), in his seminal work YuktibhÄį¹£Ä.
A proof of Brahmaguptaās method for finding area of cyclic quadrilateral is given by the Indian Hindu mathematician Jyeį¹£į¹hadeva (c.ā1500 ā c.ā1575), in his seminal work YuktibhÄį¹£Ä.
45/N
European scholars claim that Brahmagupta's method to find the area of a cyclic quadrilateral was ārediscoveredā by Dutch Mathematician Willebrord Snellius in 1619 A.D.
European scholars claim that Brahmagupta's method to find the area of a cyclic quadrilateral was ārediscoveredā by Dutch Mathematician Willebrord Snellius in 1619 A.D.
46/N
Snellius claimed it as his own invention. He wrote āwe have a very elegant theorem of this kind' and then referred to it as āthis new little theorem of mine'ā
Snellius claimed it as his own invention. He wrote āwe have a very elegant theorem of this kind' and then referred to it as āthis new little theorem of mine'ā
48/N
However any reference to a proof is absent in Snelliusās work, which makes it likely that Snellius did not have one.
However any reference to a proof is absent in Snelliusās work, which makes it likely that Snellius did not have one.
49/N
Was the method to compute area of a cyclic quadrilateral ārediscoveredā by Willebrord Snellius or did he just steal the idea from Brahmagupta without proper attribution ? Letās trace how Brahmaguptaās work reached Europe.
Was the method to compute area of a cyclic quadrilateral ārediscoveredā by Willebrord Snellius or did he just steal the idea from Brahmagupta without proper attribution ? Letās trace how Brahmaguptaās work reached Europe.
50/N
In about 770 AD, Muhammad ibn Ibrahim al-Fazari was a Muslim philosopher, mathematician. Along with YaŹæqÅ«b ibn į¹¬Äriq he helped translate the Indian astronomical text by Brahmagupta, the BrÄhmasphuį¹asiddhÄnta, into Arabic as Az-ZÄ«j āalÄ SinÄ« al-āArab. or the Sindhind.
In about 770 AD, Muhammad ibn Ibrahim al-Fazari was a Muslim philosopher, mathematician. Along with YaŹæqÅ«b ibn į¹¬Äriq he helped translate the Indian astronomical text by Brahmagupta, the BrÄhmasphuį¹asiddhÄnta, into Arabic as Az-ZÄ«j āalÄ SinÄ« al-āArab. or the Sindhind.
51/N
al-Fazariās Arabic translation of the original BrÄhmasphuį¹asiddhÄnta was the vehicle by means of which the Hindu numerals & Hindu mathematics were transmitted from India to Islamic world (continued)
al-Fazariās Arabic translation of the original BrÄhmasphuį¹asiddhÄnta was the vehicle by means of which the Hindu numerals & Hindu mathematics were transmitted from India to Islamic world (continued)
52/N
The famous Arabic scholar al-Khwarizm (780-850 AD) is known to have made use of this translation of BrÄhmasphuį¹asiddhÄnta.
The famous Arabic scholar al-Khwarizm (780-850 AD) is known to have made use of this translation of BrÄhmasphuį¹asiddhÄnta.
53/N
Around 825 CE, al-Khwarizmi wrote the manuscript, al-Jamā wa al-Tafriq bi Hisab al-Hind,
translated as āThe Book of Addition and Subtraction According to the Hindu Calculationā
Around 825 CE, al-Khwarizmi wrote the manuscript, al-Jamā wa al-Tafriq bi Hisab al-Hind,
translated as āThe Book of Addition and Subtraction According to the Hindu Calculationā
54/N
Latin translations of al-Jamā wa al-Tafriq bi Hisab al-Hind known as Algorithmi De Numero Indorum was composed in Spain around the 11th century
Latin translations of al-Jamā wa al-Tafriq bi Hisab al-Hind known as Algorithmi De Numero Indorum was composed in Spain around the 11th century
55/N
āAlgorithmi De Numero Indorumā played a crucial role in introducing the Indian geometry, mathematics and the corresponding computational methods into Europe.
āAlgorithmi De Numero Indorumā played a crucial role in introducing the Indian geometry, mathematics and the corresponding computational methods into Europe.
56/N
So it is very likely that Willebrord Snellius had access to Brahmaguptaās work via the Latin translation by the time he started working on the cyclic quadrilateral problem.
So it is very likely that Willebrord Snellius had access to Brahmaguptaās work via the Latin translation by the time he started working on the cyclic quadrilateral problem.
57/N
It took Europeans about 1000 years to even reproduce what ancient Indians discovered regarding mensuration of cyclic quadrilaterals.
It took Europeans about 1000 years to even reproduce what ancient Indians discovered regarding mensuration of cyclic quadrilaterals.
58/N
The brilliant discovery of mensurations of cyclic quadrilateral by the ancient Indian mathematicians has applications of various domains even today - including differential calculus, astronomy and computational geometry.
The brilliant discovery of mensurations of cyclic quadrilateral by the ancient Indian mathematicians has applications of various domains even today - including differential calculus, astronomy and computational geometry.
59/N
References
References
Loading suggestions...