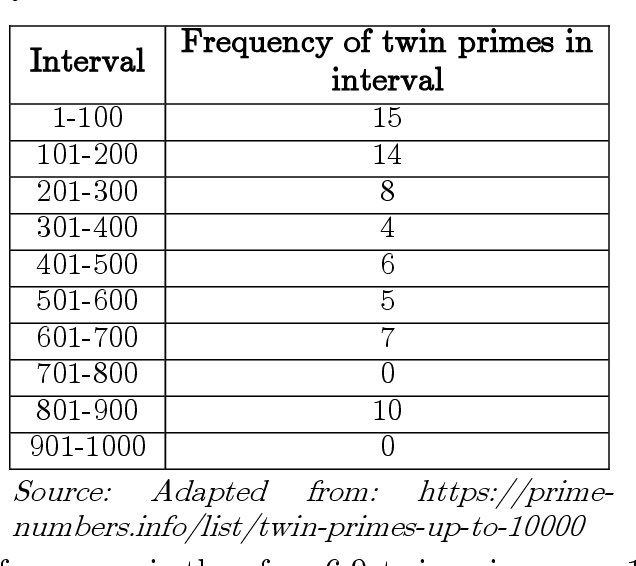
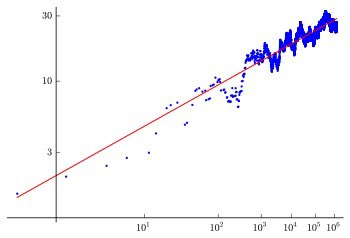
1/ Today, we'll explore some of the most famous unsolved problems in mathematics, discuss their significance, and look at the progress being made towards finding solutions. Let's dive in!
📚Book:
"SIMILARITIES BETWEEN LANDAU'S PROBLEMS: GOLDBACH'S CONJECTURE AND OTHER CONJECTURES IN NUMBER THEORY "
by Sr Javier Santos
amzn.to
"SIMILARITIES BETWEEN LANDAU'S PROBLEMS: GOLDBACH'S CONJECTURE AND OTHER CONJECTURES IN NUMBER THEORY "
by Sr Javier Santos
amzn.to
5/ The Goldbach Conjecture:
Proposed in 1742, this conjecture states that every even integer greater than 2 can be expressed as the sum of two prime numbers. Although extensively tested and widely believed to be true, no formal proof exists yet.
Proposed in 1742, this conjecture states that every even integer greater than 2 can be expressed as the sum of two prime numbers. Although extensively tested and widely believed to be true, no formal proof exists yet.
📚 Book:
"Unsolved Problems in Number Theory" (Problem Books in Mathematics, 3rd Edition) by Richard Guy
amzn.to
"Unsolved Problems in Number Theory" (Problem Books in Mathematics, 3rd Edition) by Richard Guy
amzn.to
📚 Book:
"What is the P vs NP problem?: A complete explanation of the biggest unsolved problem in Computer Science"
by Ramaswami Mohandoss
amzn.to
"What is the P vs NP problem?: A complete explanation of the biggest unsolved problem in Computer Science"
by Ramaswami Mohandoss
amzn.to
We hope you enjoyed this journey through the problems of mathematics! Be sure to check out these amazing books to explore each unsolved problem in more depth.
You can check out our other threads on Physics!
You can check out our other threads on Physics!
*Correction:
n/2 if n is even
3n+1 if n is odd
n/2 if n is even
3n+1 if n is odd
Loading suggestions...



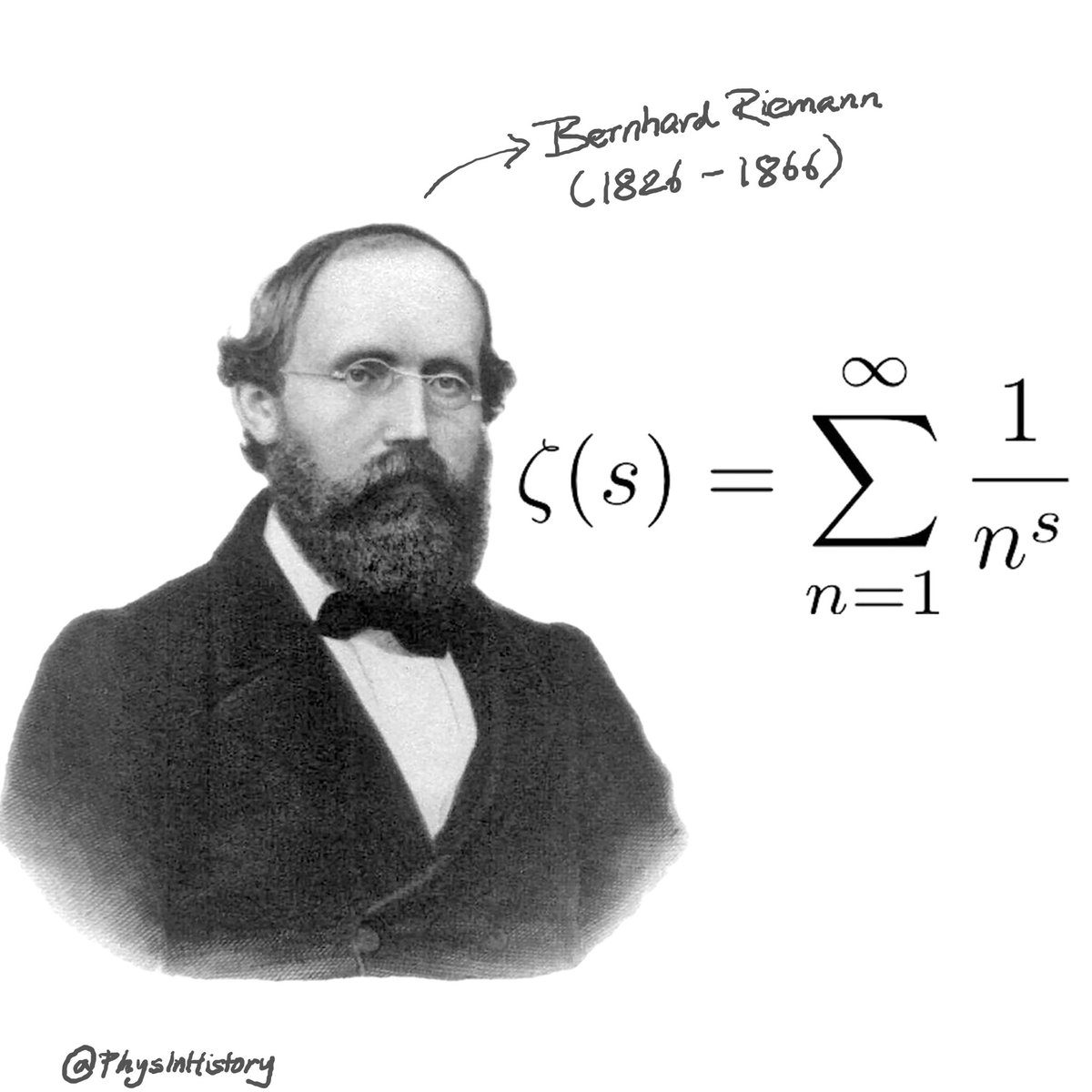










![Atoms, Stars, and Everything in Between [Science E-book] Collected Essays](https://pbs.twimg.com/news_img/1653798498100453376/NCKiih9j?format=jpg&name=orig)