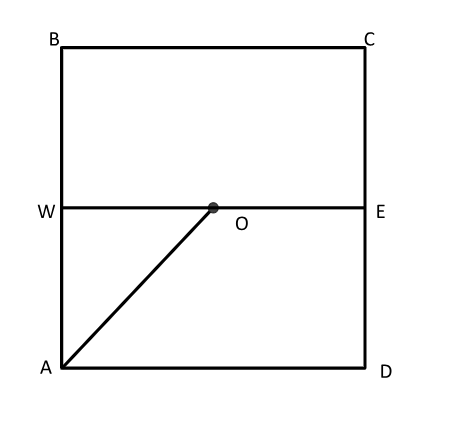1/N
This is a thread on two geometry problems: circling the square & squaring the circle. These problems were first proposed & analyzed by ancient Indian Hindus before 2000 BCE. They also designed multiple methods & provided approximate solutions before 800 BCE
This is a thread on two geometry problems: circling the square & squaring the circle. These problems were first proposed & analyzed by ancient Indian Hindus before 2000 BCE. They also designed multiple methods & provided approximate solutions before 800 BCE
2/N
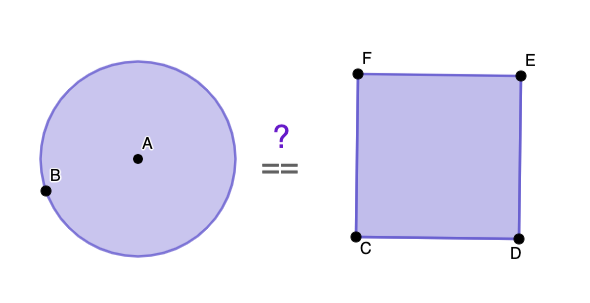
Circling the square is an important problem in geometry which refers to the problem of constructing a circle with the same area as that of a given square.
Circling the square is an important problem in geometry which refers to the problem of constructing a circle with the same area as that of a given square.
3/N
The inverse problem is known as squaring the circle, which is the problem of constructing a square with the area of a given circle.
The inverse problem is known as squaring the circle, which is the problem of constructing a square with the area of a given circle.
4/N
Both these problems were studied by the ancient Indian mathematicians since at least 2000 BCE, as we will see in this thread
Both these problems were studied by the ancient Indian mathematicians since at least 2000 BCE, as we will see in this thread
5/N
Before we delve into the actual numerical recipes that ancient Indians invented to solve these problems, we will take a brief detour and try to understand why these problems with specific geometric constraints were important to the followers of Vedic systems in India.
Before we delve into the actual numerical recipes that ancient Indians invented to solve these problems, we will take a brief detour and try to understand why these problems with specific geometric constraints were important to the followers of Vedic systems in India.
6/N
The problems of circling the square and squaring the circle were rooted in how ancient Indians looked into the process of self-realization - specifically the science & art of Yajna (เคฏเคเฅเค) - fire based rituals.
The problems of circling the square and squaring the circle were rooted in how ancient Indians looked into the process of self-realization - specifically the science & art of Yajna (เคฏเคเฅเค) - fire based rituals.
7/N
An important part of the process of performing these Yajnas is described in Shulba Sutras.
An important part of the process of performing these Yajnas is described in Shulba Sutras.
8/N
Shulba Sutras are part of Kalpa Sutras in Veclic literature, an enormous body of work dealing with means of self-realization. There are four main Shulba Sutras - Baudhayana, Apastamba, Manava, Katyayana, & a number of smaller ones.
Shulba Sutras are part of Kalpa Sutras in Veclic literature, an enormous body of work dealing with means of self-realization. There are four main Shulba Sutras - Baudhayana, Apastamba, Manava, Katyayana, & a number of smaller ones.
9/N
Shulba Sutras are used to construct physical altars for Yajna. These altars are called โchiti' in Sanskrit (เคเคฟเคคเคฟ). Chitis are complex 3D structures - construction of which requires advanced knowledge of geometrical skills.
Shulba Sutras are used to construct physical altars for Yajna. These altars are called โchiti' in Sanskrit (เคเคฟเคคเคฟ). Chitis are complex 3D structures - construction of which requires advanced knowledge of geometrical skills.
10/N
A chiti (เคเคฟเคคเคฟ) is a basis that symbolizes Chitta (เคเคฟเคคเฅเคค) or consciousness.
A chiti (เคเคฟเคคเคฟ) is a basis that symbolizes Chitta (เคเคฟเคคเฅเคค) or consciousness.
11/N
The general format for the main Shulba Sutras are the same - each starts with sections on geometrical and arithmetical constructions and ends with details of how to build โchitisโ.
The general format for the main Shulba Sutras are the same - each starts with sections on geometrical and arithmetical constructions and ends with details of how to build โchitisโ.
12/N
When the Shulba Sutras are viewed as a whole, instead of collection of parts, then a striking level of mathematical efficiency & integrity becomes apparent.
When the Shulba Sutras are viewed as a whole, instead of collection of parts, then a striking level of mathematical efficiency & integrity becomes apparent.
13/N
Literal meaning of the word Shulba is rope. In its true essence Shulba represents both connection & evolution from individual consciousness to the universal consciousness.
Literal meaning of the word Shulba is rope. In its true essence Shulba represents both connection & evolution from individual consciousness to the universal consciousness.
14/N
Agni (เค เคเฅเคจเคฟ) or fire has huge importance in Vedic knowledge system. Agni is the seer-will in the universe unerring in all its works. He is a truth conscious soul, a seer, a priest and a worker, the immortal worker in all beings.
Agni (เค เคเฅเคจเคฟ) or fire has huge importance in Vedic knowledge system. Agni is the seer-will in the universe unerring in all its works. He is a truth conscious soul, a seer, a priest and a worker, the immortal worker in all beings.
15/N
All offerings during a Yagna are made to Agni - which is the ultimate transforming agent. There are three specific เคเคฟเคคเคฟ which are of primary importance in Vedic Knowledge system.
All offerings during a Yagna are made to Agni - which is the ultimate transforming agent. There are three specific เคเคฟเคคเคฟ which are of primary importance in Vedic Knowledge system.
16/N
There are three essential เคเคฟเคคเคฟ or altars in Vedic rituals: namely เคเคพเคฐเฅเคนเคชเคคเฅเคฏ (Garhapatya), เคเคนเคตเคจเฅเคฏ (Ahavaniya) and เคฆเคเฅเคทเคฟเคฃเคพเคเฅเคจเคฟ (Dakshinagni). The fire kindled in these altars are known as Tretagni & are directly related to the geometry problems mentioned in this thread.
There are three essential เคเคฟเคคเคฟ or altars in Vedic rituals: namely เคเคพเคฐเฅเคนเคชเคคเฅเคฏ (Garhapatya), เคเคนเคตเคจเฅเคฏ (Ahavaniya) and เคฆเคเฅเคทเคฟเคฃเคพเคเฅเคจเคฟ (Dakshinagni). The fire kindled in these altars are known as Tretagni & are directly related to the geometry problems mentioned in this thread.
17/N
These three altars (Garhapatya, Ahavaniya and Dakshinagni) need to be constructed in such a way so that the bases of all of them have the same area but each base has a different shape (Garhapatya: circular, Ahavaniya: square and Dakshinagni: semi-circular)
These three altars (Garhapatya, Ahavaniya and Dakshinagni) need to be constructed in such a way so that the bases of all of them have the same area but each base has a different shape (Garhapatya: circular, Ahavaniya: square and Dakshinagni: semi-circular)
18/N
The geometric problems of circling the square & squaring the circle can be traced back to this constraint
The geometric problems of circling the square & squaring the circle can be traced back to this constraint
19/N
The earliest reference to that constraint in building these altars is found in Shatapatha Brahmana (เคถเคคเคชเคฅเคฌเฅเคฐเคพเคนเฅเคฎเคฃ) - 7.1.1.37 (no later than 2000 BCE). The original Sanskrit text of the verse & its contextual translation are provided below.
The earliest reference to that constraint in building these altars is found in Shatapatha Brahmana (เคถเคคเคชเคฅเคฌเฅเคฐเคพเคนเฅเคฎเคฃ) - 7.1.1.37 (no later than 2000 BCE). The original Sanskrit text of the verse & its contextual translation are provided below.
20/N
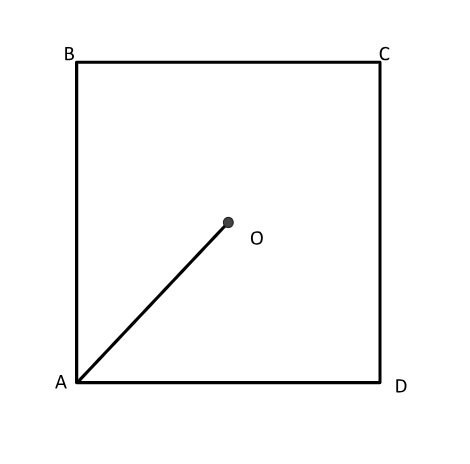
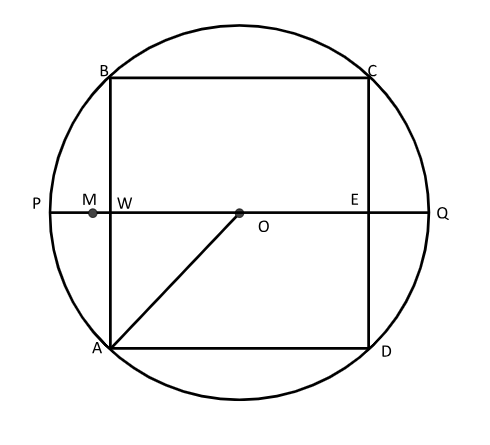
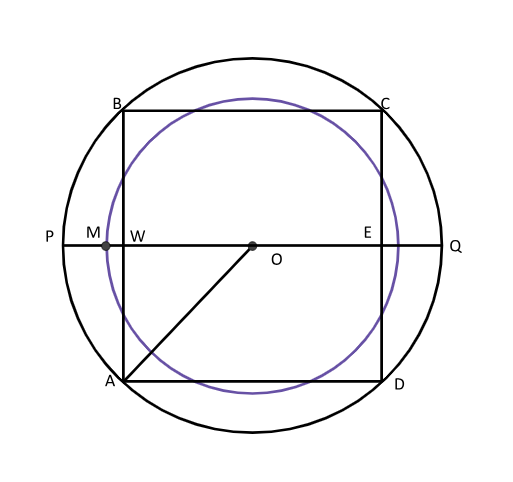
Now that we know why ancient Indians wanted to solve the problems of circling the square and squaring the circle problems, letโs look into what solutions they came up with.
Now that we know why ancient Indians wanted to solve the problems of circling the square and squaring the circle problems, letโs look into what solutions they came up with.
21/N
The first reference to an approximation solution to circling the square problem is found in the Baudhayana Shulba Sutra
The first reference to an approximation solution to circling the square problem is found in the Baudhayana Shulba Sutra
22/N
The translation of Baudhayana Shulba Sutra 1.58 for finding an approximate solution to circling the square problem is given below
The translation of Baudhayana Shulba Sutra 1.58 for finding an approximate solution to circling the square problem is given below
23/N
Letโs illustrate Baudhayanaโs method of circling the square step by step. Let ABCD be a square for which we want to find out a circle whose area is approximately the same as the area the square.
Letโs illustrate Baudhayanaโs method of circling the square step by step. Let ABCD be a square for which we want to find out a circle whose area is approximately the same as the area the square.
24/N
First we join OA
First we join OA
25/N
Then we draw an east west line by drawing a line that goes through the point C and is perpendicular to both AB and CD
Then we draw an east west line by drawing a line that goes through the point C and is perpendicular to both AB and CD
26/N
We then divide the line segment WP so that WM is one third of WP
We then divide the line segment WP so that WM is one third of WP
27/N
Finally we draw a circle with O as center and OM as radius. This is our desired circle (drawn in purple here)
Finally we draw a circle with O as center and OM as radius. This is our desired circle (drawn in purple here)
28/N
We know that the method specified in the Shulba Sutras for circling a square is meant to find an approximate solution. Letโs find out the how closely the circle estimates the given square
We know that the method specified in the Shulba Sutras for circling a square is meant to find an approximate solution. Letโs find out the how closely the circle estimates the given square
29/N
Apastamba Shulba Sutra also gives a very similar recipe for circling the square as provided in the Baudhayana Shula Sutra
Apastamba Shulba Sutra also gives a very similar recipe for circling the square as provided in the Baudhayana Shula Sutra
30/N
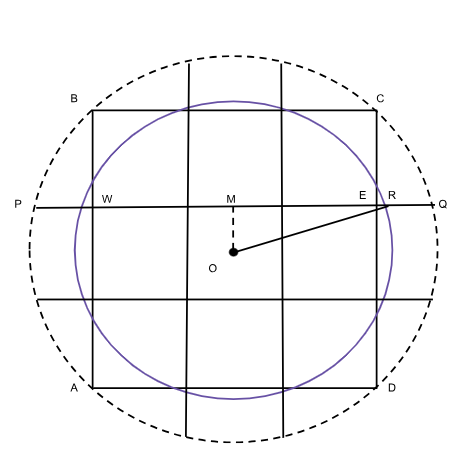
It is interesting to note that ancient Indian mathematicians were very aware of the approximate nature of this numerical recipe for circling the square
It is interesting to note that ancient Indian mathematicians were very aware of the approximate nature of this numerical recipe for circling the square
31/N
In Apastamba Shulba Sutra it is specifically mentioned that the method was provided as an approximation and not as an exact solution. Apastamba mentioned โIt is an inexact method construction of the circle; by as much as the circle falls short, so much comes inโ
In Apastamba Shulba Sutra it is specifically mentioned that the method was provided as an approximation and not as an exact solution. Apastamba mentioned โIt is an inexact method construction of the circle; by as much as the circle falls short, so much comes inโ
32/N
Manava Shulba Sutra gives an even more accurate recipe as a solution to circling the square problem
Manava Shulba Sutra gives an even more accurate recipe as a solution to circling the square problem
33/N
The translation of the above verse from the Manava Shulba Sutra is given below
The translation of the above verse from the Manava Shulba Sutra is given below
34/N
The geometrical recipe mentioned in Manava Shulba Sutra 11.15 is given below in the diagram.
The geometrical recipe mentioned in Manava Shulba Sutra 11.15 is given below in the diagram.
35/N
The construction method and error analysis of the recipe of circling the square problem in Manava Shulba Sutra is given below
The construction method and error analysis of the recipe of circling the square problem in Manava Shulba Sutra is given below
36/N
Now, we will talk about squaring the circling problem. The first reference to approximate solution of the problem is found in Baudhayana Shulba Sutra
Now, we will talk about squaring the circling problem. The first reference to approximate solution of the problem is found in Baudhayana Shulba Sutra
37/N
The translation of the recipe for squaring the circling problem as described in Baudhayana Shulba Sutra 1.10 is given below
The translation of the recipe for squaring the circling problem as described in Baudhayana Shulba Sutra 1.10 is given below
38/N
An Analysis of the solution prescribed in the Baudhayana Shulba Sutra 1.10 is given below
An Analysis of the solution prescribed in the Baudhayana Shulba Sutra 1.10 is given below
39/N
Ancient Greeks thought the problem of constructing a square whose area is that of a circle can be solved exactly rather than an approximation to it.
Ancient Greeks thought the problem of constructing a square whose area is that of a circle can be solved exactly rather than an approximation to it.
40/N
The first known Greek to study the problem was Anaxagoras (5th century BCE), who worked on it while in prison.
The first known Greek to study the problem was Anaxagoras (5th century BCE), who worked on it while in prison.
41/N
Antiphon the Sophist (5th century BC) thought that inscribing regular polygons within a circle and doubling the number of sides would eventually fill up the area of the circle
Antiphon the Sophist (5th century BC) thought that inscribing regular polygons within a circle and doubling the number of sides would eventually fill up the area of the circle
42/N
Ancient Greeks, of course failed in finding an exact solution, as it was theoretically possible.
Ancient Greeks, of course failed in finding an exact solution, as it was theoretically possible.
43/N
In 1882 CE, the LindemannโWeierstrass theorem proved that squaring the circle problem is impossible to solve if one desires an exact solution.
In 1882 CE, the LindemannโWeierstrass theorem proved that squaring the circle problem is impossible to solve if one desires an exact solution.
44/N
In summary, ancient Indians have been studying circling the square & squaring the circle problems since at least 2000 BCE. They designed an approximate solution to both these problems and utilized it to construct magnificent 3D structures.
In summary, ancient Indians have been studying circling the square & squaring the circle problems since at least 2000 BCE. They designed an approximate solution to both these problems and utilized it to construct magnificent 3D structures.
45/N
The solution to circling the square & squaring the circle problems by ancient Indians laid the foundation of many recipes for an important mathematical field which today is known as computational geometry.
The solution to circling the square & squaring the circle problems by ancient Indians laid the foundation of many recipes for an important mathematical field which today is known as computational geometry.
46/N
References
References
47/N
Correction: In 42/N of it should have said
"Ancient Greeks, of course failed in finding an exact solution, as it was theoretically impossible"
Correction: In 42/N of it should have said
"Ancient Greeks, of course failed in finding an exact solution, as it was theoretically impossible"
Loading suggestions...